1 Cup And 1 4 Divided By 2
sonusaeterna
Nov 17, 2025 · 11 min read
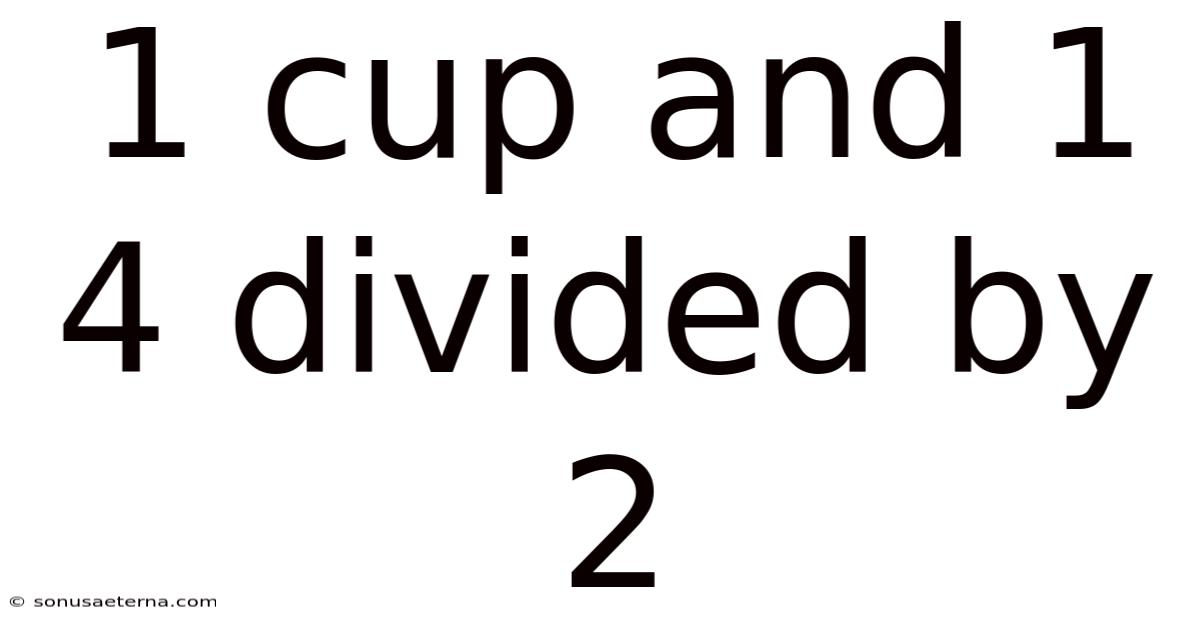
Table of Contents
Imagine you're in the kitchen, recipe book open, ready to bake your grandmother's famous cookies. You glance at the ingredient list: "1 1/4 cups of flour." But, wait a minute! You only want to make half the batch. Suddenly, you're faced with a mathematical challenge – how do you divide 1 1/4 cups by 2? It seems simple on the surface, but fractions can sometimes throw us for a loop, especially when we're trying to get precise measurements for a perfect bake.
The scenario described is a common encounter, highlighting the necessity to understand how to properly perform mathematical operations with fractions and whole numbers. Knowing how to divide 1 1/4 by 2 isn't just about baking; it’s a fundamental skill applicable to various real-life situations. From splitting resources fairly to understanding proportions in science, this mathematical operation has far-reaching relevance. In this article, we will explore a comprehensive breakdown of how to accurately divide 1 1/4 by 2, providing you with the knowledge and confidence to tackle similar mathematical problems with ease.
Main Subheading
Dividing 1 1/4 by 2 might seem straightforward, but it involves a few key steps to ensure accuracy. At its core, this problem requires understanding how to divide a mixed number by a whole number. A mixed number, like 1 1/4, combines a whole number and a fraction, which can sometimes complicate the division process. The goal is to break down this mixed number into a more manageable form, typically an improper fraction, before performing the division. This preliminary step simplifies the calculations and reduces the chances of error.
Once the mixed number is converted into an improper fraction, dividing by a whole number becomes much easier. The fundamental principle here is that dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 2, for instance, is 1/2. This transformation allows us to convert the division problem into a multiplication problem, which is often more intuitive and less prone to errors. By understanding and applying these steps, dividing 1 1/4 by 2 becomes a manageable task that can be performed with precision and confidence.
Comprehensive Overview
To understand how to divide 1 1/4 by 2, let’s delve into the definitions, scientific foundations, history, and essential concepts related to this mathematical operation.
Definitions:
- Fraction: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 1/4, 1 is the numerator, and 4 is the denominator.
- Mixed Number: A mixed number is a combination of a whole number and a fraction, such as 1 1/4. It represents a quantity greater than one whole.
- Improper Fraction: An improper fraction is a fraction where the numerator is greater than or equal to the denominator, such as 5/4. It also represents a quantity greater than or equal to one whole.
- Reciprocal: The reciprocal of a number is 1 divided by that number. For example, the reciprocal of 2 is 1/2, and the reciprocal of 1/4 is 4/1, or simply 4.
Scientific Foundations:
The scientific foundation for understanding fractions and division lies in the principles of arithmetic, which is a branch of mathematics dealing with the properties and manipulation of numbers. Dividing by a number is mathematically equivalent to multiplying by its reciprocal. This concept is rooted in the properties of multiplicative inverses, which are fundamental to algebraic structures.
History:
The concept of fractions dates back to ancient civilizations. Egyptians and Mesopotamians used fractions for practical purposes such as measuring land, dividing resources, and calculating taxes. The Egyptians, for example, used unit fractions (fractions with a numerator of 1) extensively. The Babylonians used a base-60 number system, which facilitated the use of fractions in their astronomical calculations.
The formalization of fraction arithmetic came later, with contributions from Greek mathematicians like Euclid and Archimedes. The development of a consistent notation and rules for operating with fractions was crucial for advancements in mathematics, science, and engineering. Over time, the understanding and manipulation of fractions became an essential part of mathematical education and practical problem-solving.
Essential Concepts:
- Converting Mixed Numbers to Improper Fractions: To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction, add the numerator, and then place the result over the original denominator. For example, to convert 1 1/4 to an improper fraction: (1 * 4) + 1 = 5. So, 1 1/4 = 5/4.
- Dividing Fractions: Dividing by a fraction is the same as multiplying by its reciprocal. To divide a fraction by another fraction, invert the second fraction (find its reciprocal) and then multiply the first fraction by this reciprocal. For example, to divide 1/2 by 1/4, you would multiply 1/2 by 4/1, which equals 4/2 or 2.
- Dividing by Whole Numbers: Dividing a fraction by a whole number is equivalent to multiplying the fraction by the reciprocal of the whole number. For example, to divide 1/4 by 2, you would multiply 1/4 by 1/2, which equals 1/8.
- Simplifying Fractions: Simplifying a fraction involves reducing it to its lowest terms. This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, the fraction 4/8 can be simplified by dividing both 4 and 8 by their GCD, which is 4. This results in the simplified fraction 1/2.
Understanding these definitions, historical context, and essential concepts provides a solid foundation for tackling the problem of dividing 1 1/4 by 2. The next sections will guide you through the specific steps to solve this problem accurately.
Trends and Latest Developments
In recent years, there has been a renewed emphasis on mathematical literacy and numeracy skills. Educational trends highlight the importance of mastering basic arithmetic operations, including fractions, to succeed in various fields. Data from educational assessments consistently show that many students struggle with fraction arithmetic, underscoring the need for improved teaching methods and resources.
One popular trend is the use of visual aids and manipulatives to help students understand fractions. For example, fraction bars, pie charts, and interactive simulations are used to make abstract concepts more concrete. These tools help students visualize fractions and understand how they relate to each other.
Another trend is the integration of technology into math education. Online platforms and mobile apps offer interactive lessons, practice problems, and immediate feedback, making learning more engaging and personalized. These resources often include step-by-step solutions and explanations, which can be particularly helpful for students who struggle with specific topics.
Professional insights from educators and mathematicians emphasize the importance of conceptual understanding over rote memorization. Instead of simply memorizing rules and procedures, students should understand the underlying principles and reasoning behind mathematical operations. This approach helps students develop a deeper and more flexible understanding of mathematics, which can be applied to a wider range of problems.
Tips and Expert Advice
Dividing 1 1/4 by 2 can be approached in a few ways, but the most straightforward method involves converting the mixed number to an improper fraction and then multiplying by the reciprocal of the whole number. Here are some tips and expert advice to ensure accuracy and understanding:
-
Convert the Mixed Number to an Improper Fraction:
- The first step is to convert the mixed number 1 1/4 into an improper fraction. To do this, multiply the whole number (1) by the denominator (4) and add the numerator (1). This gives you (1 * 4) + 1 = 5. The improper fraction is therefore 5/4.
- Why this works: Converting to an improper fraction makes the number easier to manipulate in multiplication and division. It represents the entire quantity as a single fraction, rather than a combination of a whole number and a fraction.
-
Understand the Reciprocal:
- Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 2 is 1/2.
- Why this works: This is a fundamental principle in arithmetic. When you divide by a number, you're essentially asking how many times that number fits into the quantity you're dividing. Multiplying by the reciprocal achieves the same result, but through multiplication, which is often easier to handle.
-
Multiply the Improper Fraction by the Reciprocal:
- Now, multiply the improper fraction (5/4) by the reciprocal of 2 (which is 1/2). So, the calculation becomes (5/4) * (1/2) = 5/8.
- Why this works: Multiplying fractions involves multiplying the numerators together and the denominators together. In this case, 5 * 1 = 5, and 4 * 2 = 8, resulting in the fraction 5/8.
-
Simplify the Result, if Necessary:
- In this case, the fraction 5/8 is already in its simplest form because 5 and 8 do not have any common factors other than 1.
- Why this works: Simplifying fractions makes them easier to understand and compare. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1.
-
Alternative Approach: Distribute the Division:
- An alternative method is to distribute the division. Divide the whole number part and the fractional part separately by 2.
- Divide the whole number 1 by 2, which gives you 1/2.
- Divide the fraction 1/4 by 2, which is the same as multiplying 1/4 by 1/2, resulting in 1/8.
- Add the two results together: 1/2 + 1/8. To add these fractions, find a common denominator, which is 8. Convert 1/2 to 4/8.
- Now add the fractions: 4/8 + 1/8 = 5/8.
- Why this works: Distributing the division can be useful for understanding the problem conceptually, breaking it down into smaller, more manageable parts.
-
Use Visual Aids:
- Draw a pie chart or use fraction bars to visualize 1 1/4. Then, divide the whole into two equal parts and the fraction into two equal parts. This can help you see that half of 1 1/4 is indeed 5/8.
- Why this works: Visual aids provide a concrete representation of the problem, making it easier to understand and solve. They can be particularly helpful for visual learners.
-
Check Your Work:
- To check your answer, you can multiply the result (5/8) by 2 to see if you get back the original number (1 1/4).
- (5/8) * 2 = 10/8, which simplifies to 5/4, and 5/4 is equal to 1 1/4.
- Why this works: Checking your work ensures that you have performed the calculations correctly. Multiplying the result by the divisor should give you back the original dividend.
FAQ
Q: What is a mixed number, and how do I convert it to an improper fraction?
A: A mixed number is a combination of a whole number and a fraction, such as 1 1/4. To convert it to an improper fraction, multiply the whole number by the denominator, add the numerator, and place the result over the original denominator. For 1 1/4, this would be (1 * 4) + 1 = 5, so the improper fraction is 5/4.
Q: Why do we convert mixed numbers to improper fractions before dividing?
A: Converting to an improper fraction makes it easier to perform multiplication and division. It represents the entire quantity as a single fraction, simplifying the calculations and reducing the chances of error.
Q: What does it mean to find the reciprocal of a number?
A: The reciprocal of a number is 1 divided by that number. For example, the reciprocal of 2 is 1/2, and the reciprocal of 1/4 is 4. Finding the reciprocal is essential for converting division problems into multiplication problems.
Q: How do I divide a fraction by a whole number?
A: Dividing a fraction by a whole number is the same as multiplying the fraction by the reciprocal of the whole number. For example, to divide 1/4 by 2, you would multiply 1/4 by 1/2, which equals 1/8.
Q: Can I use a calculator to divide fractions?
A: Yes, you can use a calculator to divide fractions. Most calculators have a fraction function or can handle decimal equivalents of fractions. However, understanding the underlying principles of fraction arithmetic is crucial for problem-solving and conceptual understanding.
Conclusion
Dividing 1 1/4 by 2 requires a clear understanding of fractions, mixed numbers, and the principles of division. By converting the mixed number to an improper fraction, understanding the concept of reciprocals, and performing the multiplication accurately, we arrive at the result: 5/8. This process not only provides the correct answer but also enhances our ability to solve similar mathematical problems in various real-world scenarios.
Now that you've mastered dividing 1 1/4 by 2, put your skills to the test! Try similar problems with different fractions and whole numbers. Share your solutions and insights in the comments below, and let's continue to learn and grow together. Your engagement and practice will solidify your understanding and boost your confidence in tackling mathematical challenges.
Latest Posts
Latest Posts
-
Ast To Alt Ratio Greater Than 1
Nov 17, 2025
-
What Is 2 3 Of 2 3 Cup
Nov 17, 2025
-
Newtons Method To Find Square Root
Nov 17, 2025
-
What Is The Greatest Common Factor Of 18 And 24
Nov 17, 2025
-
Difference Between Public Ip And Private Ip
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about 1 Cup And 1 4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.