What Is 2/3 Of 2/3 Cup
sonusaeterna
Nov 17, 2025 · 8 min read
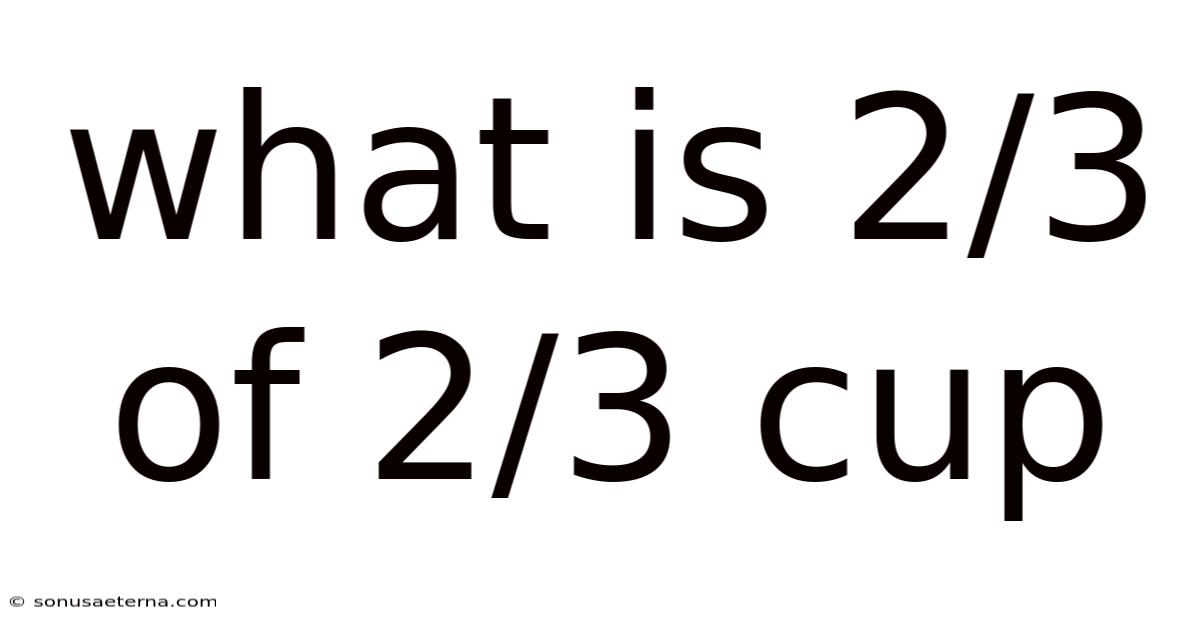
Table of Contents
Imagine you're baking your favorite chocolate chip cookies. The recipe calls for 2/3 of a cup of flour, but you want to make a smaller batch. You only want to use 2/3 of that amount. Suddenly, you're faced with a fraction problem! Don't worry, figuring out what is 2/3 of 2/3 cup isn't as daunting as it seems.
Understanding fractions is a fundamental skill that extends beyond the kitchen. From measuring ingredients in recipes to calculating proportions in construction, fractions are essential in everyday life. Mastering this concept allows you to precisely manage quantities, ensuring accuracy and efficiency in various tasks. So, let's dive into the world of fractions and unravel the mystery of calculating a fraction of a fraction.
Main Subheading
Before we tackle the specific question of what is 2/3 of 2/3 cup, it's important to understand the basic concept. Finding a fraction of something essentially means multiplying that fraction by the original value. In our case, we're finding 2/3 of 2/3 cup. This is a straightforward multiplication problem that will give us the answer.
This concept is not limited to fractions within a cup. It applies to any unit of measurement, be it length, weight, volume, or even time. When you encounter a problem asking for a fraction of a fraction, remember that it fundamentally boils down to multiplication. With a clear grasp of this principle, you can confidently solve a wide range of problems involving fractional quantities.
Comprehensive Overview
To fully grasp how to calculate 2/3 of 2/3 cup, let's delve into the underlying principles of fraction multiplication. A fraction consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator represents the number of parts you have, while the denominator represents the total number of equal parts that make up the whole.
When multiplying fractions, the rule is simple: multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. Mathematically, this is expressed as: (a/b) * (c/d) = (ac) / (bd). Applying this to our question, we have (2/3) * (2/3). Multiplying the numerators (2 * 2) gives us 4, and multiplying the denominators (3 * 3) gives us 9. Therefore, 2/3 of 2/3 equals 4/9.
So, 2/3 of 2/3 cup is 4/9 cup. But what does this mean? Imagine dividing a cup into nine equal parts. Four of those parts would represent 4/9 of a cup. This gives you a tangible sense of the quantity we're dealing with. It's less than half a cup, but more than a third.
Understanding fraction multiplication is crucial not only for solving mathematical problems but also for understanding ratios and proportions. It allows you to scale recipes, calculate discounts, and understand data presented in fractional forms. The ability to confidently manipulate fractions is a valuable skill in numerous areas of life.
Fractions have been used since ancient times, with evidence of fractional notation found in ancient Egyptian and Mesopotamian texts. The concept of dividing a whole into equal parts is fundamental to human understanding of quantity and measurement. Over centuries, different cultures have developed various notations and methods for working with fractions, eventually leading to the standardized notation we use today. The development of fractions has played a crucial role in the advancement of mathematics, science, and engineering, enabling precise calculations and accurate representations of the world around us.
Trends and Latest Developments
While the basic principles of fraction multiplication remain constant, the way we interact with fractions is evolving. Calculators and software can instantly perform complex fraction calculations, but the importance of understanding the underlying concepts remains. There is a growing emphasis on teaching fractions through visual aids and hands-on activities, making the learning process more intuitive and engaging.
Educational research is also exploring how to address common misconceptions about fractions. For example, many students struggle with the idea that a fraction with a larger denominator represents a smaller quantity. By using real-world examples and interactive simulations, educators are helping students develop a deeper and more accurate understanding of fractions.
Furthermore, the use of fractions extends to modern fields like computer science and data analysis. For instance, probabilities are often expressed as fractions, and understanding fractional data is crucial for interpreting statistical results. In an increasingly data-driven world, the ability to confidently work with fractions remains a valuable asset.
Tips and Expert Advice
Here are some practical tips and expert advice to help you master working with fractions and specifically, figuring out "what is 2/3 of 2/3 cup?"
-
Visualize the Fractions: Use visual aids like pie charts or fraction bars to represent fractions. This can make it easier to understand the relative size of different fractions and how they relate to each other. For the 2/3 of 2/3 cup example, imagine a pie cut into three slices, with two slices representing 2/3. Now, imagine taking 2/3 of those two slices. You'll visually see that you end up with less than half of the whole pie. This visual representation reinforces the concept that 2/3 of 2/3 is less than 2/3.
-
Simplify Before Multiplying: If possible, simplify the fractions before multiplying them. Simplifying fractions involves dividing both the numerator and denominator by their greatest common factor. While it doesn't change the final answer in the 2/3 of 2/3 cup case (since 2/3 is already in its simplest form), simplifying fractions in more complex calculations can make the multiplication process easier and reduce the risk of errors. For example, if you were calculating 4/6 of 3/8, you could simplify 4/6 to 2/3 and 3/8 remains as is, before multiplying.
-
Use Real-World Examples: Connect fractions to real-world scenarios to make them more relatable and understandable. In addition to cooking and baking, consider examples like dividing a pizza among friends, measuring lumber for a carpentry project, or calculating discounts at a store. These examples help solidify the practical application of fractions and make them less abstract.
-
Practice Regularly: Like any mathematical skill, mastering fractions requires consistent practice. Work through various problems involving fraction multiplication, addition, subtraction, and division. Use online resources, textbooks, or worksheets to reinforce your understanding and build confidence. Even a few minutes of practice each day can make a significant difference.
-
Don't Be Afraid to Ask for Help: If you're struggling with fractions, don't hesitate to ask for help from teachers, tutors, or online communities. Explaining your difficulties can help identify areas where you need more support, and getting guidance from others can clarify confusing concepts and provide alternative approaches to problem-solving. Remember, everyone learns at their own pace, and seeking help is a sign of strength, not weakness.
FAQ
Q: What does "of" mean in math when dealing with fractions?
A: In mathematics, particularly when dealing with fractions, the word "of" typically indicates multiplication. So, when you see "2/3 of 2/3," it means 2/3 multiplied by 2/3.
Q: Is 2/3 of 2/3 bigger or smaller than 2/3?
A: 2/3 of 2/3 is smaller than 2/3. When you multiply a fraction by another fraction that is less than 1, the result will always be smaller than the original fraction.
Q: Can I use a calculator to solve this?
A: Yes, you can use a calculator to multiply fractions. Simply enter the fractions as decimals or use the fraction function on your calculator if it has one. However, understanding the underlying process is still important for problem-solving.
Q: Are there any other ways to visualize 2/3 of 2/3?
A: Yes! You can visualize it as an area. Draw a square. Divide it into 3 equal columns. Shade 2 of those columns (representing 2/3). Now, divide the same square into 3 equal rows. Highlight 2 of those rows. The area where the shading and highlighting overlap represents 2/3 of 2/3. You'll see that 4 out of the 9 smaller squares are overlapped, representing 4/9.
Q: What if I need to find a fraction of a mixed number?
A: First, convert the mixed number into an improper fraction. For example, 1 1/2 would become 3/2. Then, multiply the fractions as usual.
Conclusion
Calculating "what is 2/3 of 2/3 cup" is a practical example of fraction multiplication. Remember that "of" signifies multiplication, and the rule is to multiply the numerators and the denominators. This gives us the answer: 4/9 cup. Understanding the underlying concepts of fractions empowers you to tackle various real-world problems, from baking and cooking to more complex calculations.
Now that you've mastered this concept, put your newfound knowledge to the test! Try solving similar problems with different fractions, or apply your understanding to a real-world scenario. Share your solutions in the comments below, and let's continue to learn and grow together. What are some other situations where knowing how to calculate fractions helps you? Share your thoughts!
Latest Posts
Latest Posts
-
Speaking Of Yourself In Third Person
Nov 17, 2025
-
Free Cna Practice Test With Answers
Nov 17, 2025
-
What Does Lt Stand For In Measurement
Nov 17, 2025
-
An Important Component Of Psychoanalysis Is
Nov 17, 2025
-
Hernando De Soto Years Of Exploration
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 2/3 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.