1 3 X 2 3 X 1 2
sonusaeterna
Nov 27, 2025 · 11 min read
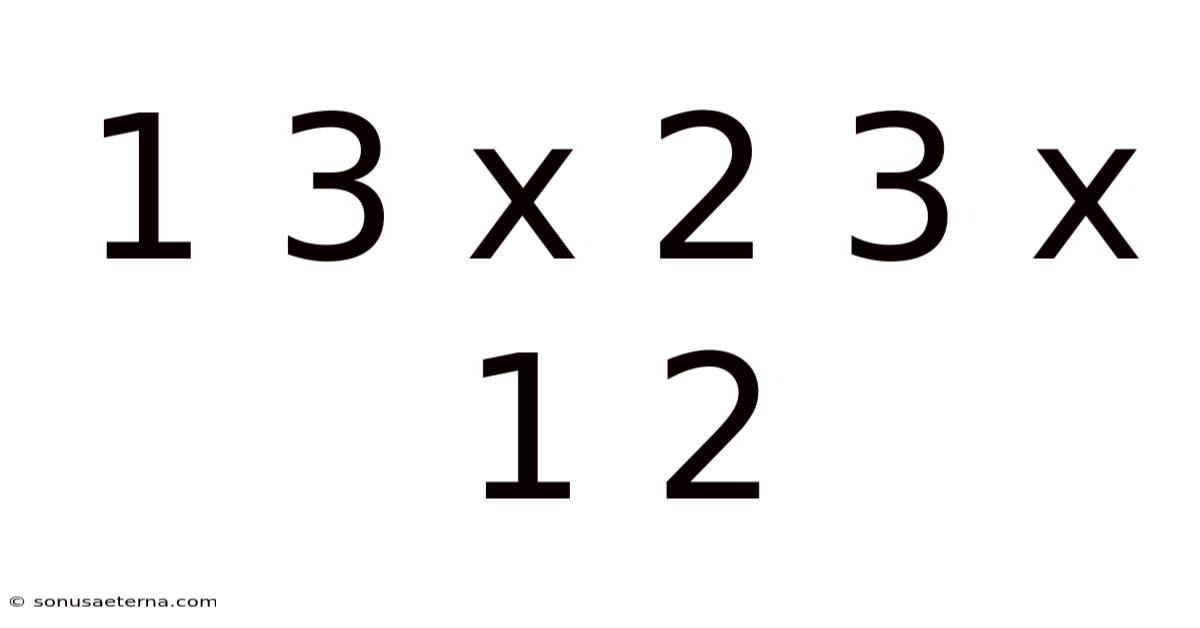
Table of Contents
Imagine you're a baker trying to figure out how much flour you need for a batch of cookies. You know you need 1 ⅓ cups of flour, but you're planning on tripling the recipe and then halving it for a smaller gathering. To figure out the exact amount, you’ll need to understand how to multiply these mixed fractions.
Similarly, in construction, a builder might need to calculate the amount of lumber required for a project. If they start with a base length of 1 ⅓ meters, increase it by a factor of 2 ⅔, and then adjust it again by ½, accurate multiplication is crucial. This type of calculation isn't just theoretical; it's a practical skill used in everyday life.
Understanding 1 ⅓ x 2 ⅔ x ½
At its core, the expression 1 ⅓ x 2 ⅔ x ½ represents the multiplication of three fractional numbers. Two of these are mixed fractions (a whole number combined with a proper fraction), and one is a simple fraction. Before we dive into solving this, it’s important to grasp the foundational concepts that make it all work. The expression may seem straightforward, but understanding the process thoroughly helps in tackling more complex mathematical problems.
When dealing with mixed fractions, the first step is to convert them into improper fractions. An improper fraction is one where the numerator (the top number) is larger than or equal to the denominator (the bottom number). This conversion is essential because it simplifies the multiplication process. Multiplying fractions involves multiplying the numerators together to get the new numerator and multiplying the denominators together to get the new denominator.
Basic Definitions and Concepts
To fully understand 1 ⅓ x 2 ⅔ x ½, let’s define some key terms and concepts:
- Fraction: A fraction represents a part of a whole. It consists of two parts: the numerator and the denominator. For example, in the fraction ½, 1 is the numerator and 2 is the denominator.
- Mixed Fraction: A mixed fraction is a combination of a whole number and a proper fraction (where the numerator is less than the denominator). 1 ⅓ is a mixed fraction.
- Improper Fraction: An improper fraction is one where the numerator is greater than or equal to the denominator, such as 4/3.
- Multiplication of Fractions: To multiply fractions, you multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator. For example, (a/b) x (c/d) = (a x c) / (b x d).
The scientific foundation behind multiplying fractions lies in the basic principles of arithmetic. Fractions represent division, and multiplying them is akin to performing successive divisions or finding a fraction of a fraction. The conversion of mixed fractions to improper fractions is based on the idea that a mixed fraction is a shorthand way of writing a whole number plus a fraction.
Historical Context
The concept of fractions dates back to ancient civilizations. Egyptians used fractions as early as 3000 BC, primarily with unit fractions (fractions with a numerator of 1). The Babylonians used a base-60 number system, which led to their use of sexagesimal fractions (fractions with a denominator of 60).
The formalization of fraction arithmetic, including multiplication, developed over centuries. Indian mathematicians, such as Aryabhata in the 5th century AD, made significant contributions to understanding and manipulating fractions. The Arabs, during the Islamic Golden Age, further refined these concepts and transmitted them to Europe.
In Europe, the widespread use of fractions became more common during the Renaissance, as trade and commerce demanded more precise calculations. Mathematicians like Fibonacci helped popularize the Hindu-Arabic numeral system, which included fractions, through his book Liber Abaci in 1202. The notation and methods we use today for multiplying fractions are a result of this long historical evolution.
Converting Mixed Fractions to Improper Fractions
Converting mixed fractions to improper fractions is a crucial step in solving our multiplication problem. Here's how to do it:
- Multiply the whole number by the denominator of the fractional part.
- Add the numerator of the fractional part to the result.
- Place the result over the original denominator.
For 1 ⅓:
- Multiply 1 (the whole number) by 3 (the denominator): 1 x 3 = 3
- Add 1 (the numerator): 3 + 1 = 4
- Place 4 over the original denominator 3: 4/3
So, 1 ⅓ is equal to 4/3.
For 2 ⅔:
- Multiply 2 (the whole number) by 3 (the denominator): 2 x 3 = 6
- Add 2 (the numerator): 6 + 2 = 8
- Place 8 over the original denominator 3: 8/3
So, 2 ⅔ is equal to 8/3.
Now we have converted our mixed fractions into improper fractions, making our original expression:
4/3 x 8/3 x ½
Multiplying the Fractions
Now that all the numbers are in fractional form, we can proceed with the multiplication. To multiply fractions, we multiply the numerators together and the denominators together:
(4/3) x (8/3) x (½) = (4 x 8 x 1) / (3 x 3 x 2)
Multiplying the numerators: 4 x 8 x 1 = 32
Multiplying the denominators: 3 x 3 x 2 = 18
So, the result is 32/18.
Simplifying the Result
The final step is to simplify the fraction 32/18. Simplifying a fraction means reducing it to its lowest terms. To do this, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it.
The GCD of 32 and 18 is 2.
Dividing both the numerator and the denominator by 2:
32 ÷ 2 = 16 18 ÷ 2 = 9
So, the simplified fraction is 16/9.
We can also convert this improper fraction back into a mixed fraction to make it more understandable. To do this, we divide the numerator by the denominator and express the remainder as a fraction:
16 ÷ 9 = 1 with a remainder of 7
So, 16/9 is equal to 1 7/9.
Therefore, 1 ⅓ x 2 ⅔ x ½ = 1 7/9
Trends and Latest Developments
In recent years, there has been a renewed focus on mathematics education, particularly in making math more accessible and relevant to everyday life. The traditional emphasis on rote memorization is gradually being replaced by teaching methods that prioritize conceptual understanding and practical application.
Educational platforms and apps are increasingly using interactive tools to teach fraction arithmetic. These tools often include visual aids, such as pie charts and bar graphs, to help students visualize fractions and understand the underlying concepts. Gamification is also a popular trend, with educational games designed to make learning math fun and engaging.
Data from educational research indicates that students who have a strong conceptual understanding of fractions perform better in algebra and other advanced math courses. This underscores the importance of mastering fraction arithmetic early in the educational journey. Additionally, there is a growing recognition of the need to address math anxiety, which can hinder students' ability to learn and apply mathematical concepts effectively. Strategies to reduce math anxiety include creating a supportive learning environment, providing personalized feedback, and emphasizing the relevance of math to real-world problems.
From a professional perspective, the ability to work with fractions is essential in various fields, including engineering, finance, and construction. In engineering, accurate calculations involving fractions are crucial for designing structures and machines. In finance, understanding fractions is necessary for calculating interest rates and investment returns. In construction, precise measurements involving fractions are essential for ensuring that buildings are structurally sound.
Tips and Expert Advice
Mastering fraction arithmetic doesn't have to be daunting. Here are some practical tips and expert advice to help you improve your skills:
- Start with the Basics: Ensure you have a solid understanding of what fractions represent. Use visual aids like pie charts or fraction bars to help visualize fractions and understand their relative sizes. Understanding the basics is the foundation for tackling more complex problems.
- Practice Converting Mixed Fractions and Improper Fractions: As seen in the example 1 ⅓ x 2 ⅔ x ½, being able to convert between mixed fractions and improper fractions quickly and accurately is essential. Practice this skill regularly until it becomes second nature. Use online resources or create your own practice problems.
- Use Real-World Examples: Relate fraction arithmetic to real-world situations to make it more meaningful. For example, think about splitting a pizza among friends or measuring ingredients for a recipe. The more you can connect fractions to your daily life, the easier they will be to understand.
- Break Down Complex Problems: When faced with a complex problem involving multiple fractions, break it down into smaller, more manageable steps. This will make the problem less intimidating and easier to solve. For example, in the problem 1 ⅓ x 2 ⅔ x ½, we first converted the mixed fractions to improper fractions, then multiplied the fractions, and finally simplified the result.
- Use Online Resources and Tools: There are many excellent online resources and tools available to help you learn and practice fraction arithmetic. Websites like Khan Academy, Mathway, and Symbolab offer tutorials, practice problems, and step-by-step solutions. Take advantage of these resources to supplement your learning.
- Focus on Understanding the Concepts: Rather than memorizing rules and formulas, focus on understanding the underlying concepts. This will help you apply your knowledge to different types of problems and remember the rules more easily. For example, understand why we convert mixed fractions to improper fractions before multiplying them.
- Practice Regularly: Like any skill, mastering fraction arithmetic requires regular practice. Set aside time each day or week to work on fraction problems. The more you practice, the more confident and proficient you will become.
- Check Your Work: Always double-check your work to ensure that you have made no errors. This is especially important when dealing with complex problems involving multiple steps. Use a calculator or online tool to verify your answers.
- Seek Help When Needed: Don't be afraid to ask for help if you are struggling with fraction arithmetic. Talk to your teacher, a tutor, or a friend who is good at math. Getting help from others can provide you with new insights and perspectives.
- Stay Positive: Learning math can be challenging, but it is important to stay positive and persistent. Believe in your ability to learn and improve, and don't get discouraged by mistakes. Every mistake is an opportunity to learn and grow.
FAQ
Q: Why do we need to convert mixed fractions to improper fractions before multiplying?
A: Converting mixed fractions to improper fractions simplifies the multiplication process. When you multiply mixed fractions directly, it can be confusing and lead to errors. By converting them to improper fractions, you can easily multiply the numerators and denominators to get the correct result.
Q: How do you simplify a fraction?
A: To simplify a fraction, you find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. This reduces the fraction to its lowest terms.
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 5/3 is an improper fraction.
Q: How do you convert an improper fraction back to a mixed fraction?
A: To convert an improper fraction back to a mixed fraction, you divide the numerator by the denominator. The quotient becomes the whole number part of the mixed fraction, and the remainder becomes the numerator of the fractional part. The denominator remains the same.
Q: Are fractions used in real life?
A: Yes, fractions are used extensively in real life. They are used in cooking, baking, construction, finance, and many other fields. Understanding fractions is essential for everyday tasks such as splitting a bill, measuring ingredients, and calculating discounts.
Q: What if I have more than three fractions to multiply?
A: The process is the same regardless of how many fractions you have. Multiply all the numerators together to get the new numerator and multiply all the denominators together to get the new denominator. Then, simplify the resulting fraction if possible.
Q: Can I use a calculator to multiply fractions?
A: Yes, you can use a calculator to multiply fractions. Most calculators have a fraction function that allows you to enter and multiply fractions easily. However, it is still important to understand the underlying concepts and be able to perform the calculations manually.
Conclusion
In this article, we've explored the process of multiplying fractions, specifically the expression 1 ⅓ x 2 ⅔ x ½. We discussed the importance of converting mixed fractions to improper fractions, the steps involved in multiplying fractions, and how to simplify the final result. Understanding these concepts is crucial for anyone looking to improve their math skills and apply them in real-world situations.
By following the tips and advice provided, you can master fraction arithmetic and gain confidence in your ability to solve mathematical problems. Remember to start with the basics, practice regularly, and seek help when needed. With dedication and perseverance, you can overcome any challenges and achieve your goals.
Now that you have a solid understanding of multiplying fractions, take the next step and apply your knowledge to solve real-world problems. Try calculating the amount of ingredients needed for a recipe or figuring out the dimensions of a room. The more you practice, the more proficient you will become. Share this article with friends or family who might benefit from it, and leave a comment below with your own tips and experiences with fraction arithmetic. Let's continue to learn and grow together!
Latest Posts
Latest Posts
-
Why Does The Right Lung Have 3 Lobes
Nov 27, 2025
-
What Is 2 Pi R Squared
Nov 27, 2025
-
An Atom Is Electrically Neutral Because
Nov 27, 2025
-
What Is The Function Of The Bacterial Cell Wall
Nov 27, 2025
-
Physical Features Of The Southwest Region
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about 1 3 X 2 3 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.