What Is 2 Pi R Squared
sonusaeterna
Nov 27, 2025 · 11 min read
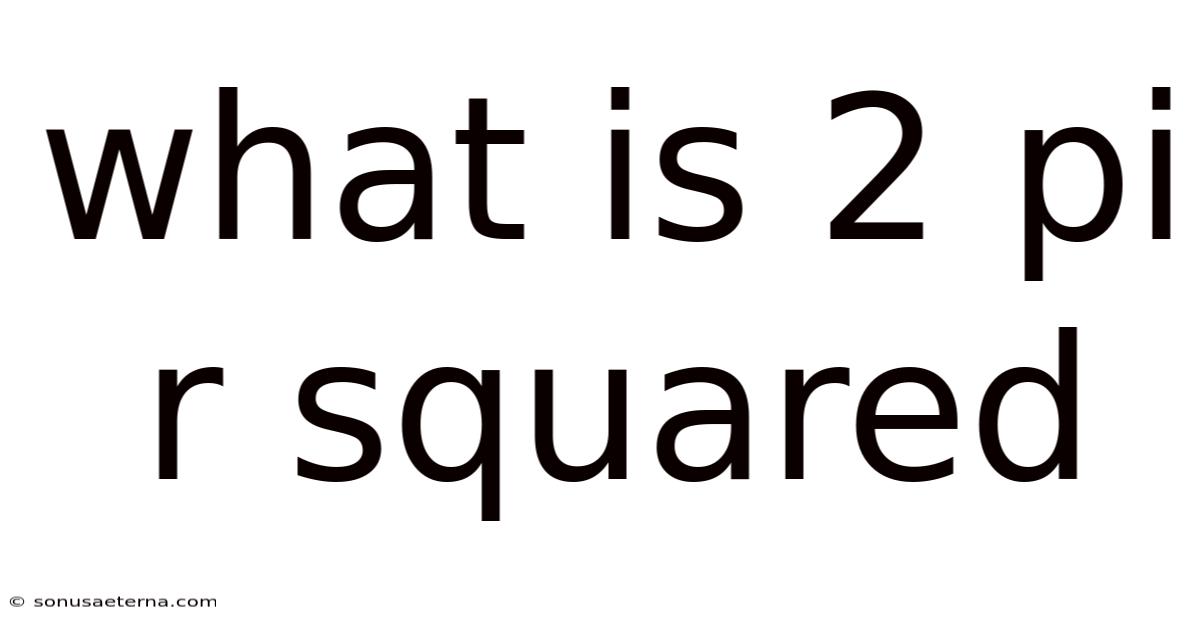
Table of Contents
Imagine holding a perfectly round pizza, ready to slice it up and share with friends. Before you make those cuts, think about figuring out how much sauce you'll need to cover the entire surface. That’s where the formula 2πr squared comes in handy. But wait, that sounds like the area of a circle, which is πr squared. So what exactly is 2πr squared?
Well, let's switch from pizzas to beach balls. The amount of material needed to make that beach ball, the outer surface we can touch, is what 2πr squared helps us calculate. If the pizza was a ball, 2πr squared wouldn't tell us about the sauce on top (the area) but about the ball's skin. This formula isn't about flat circles; it's about spheres, like our planet Earth, and understanding their surfaces.
Understanding 2πr Squared: The Surface Area of a Hemisphere
At its core, 2πr squared represents the surface area of a hemisphere – precisely, one half of a sphere including its circular base. To truly understand what this means, it’s essential to break down each component of the formula and explore the geometric principles that support it. This understanding isn't just about memorizing a formula; it's about visualizing shapes in three dimensions and grasping the relationship between different geometric properties.
The formula connects fundamental geometric concepts to tangible, real-world applications. Whether it's calculating how much paint is needed to coat a dome-shaped roof or determining the amount of material required to produce spherical containers, 2πr squared provides essential insights. By delving into its components and applications, we gain a deeper appreciation for the elegance and utility of mathematics in describing and interacting with the world around us.
Comprehensive Overview of 2πr Squared
To fully grasp the significance of 2πr squared, we need to dissect its components and understand the geometric principles behind it:
-
π (Pi): Pi is a mathematical constant approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter. Pi is ubiquitous in mathematics and physics, appearing in formulas related to circles, spheres, cylinders, and various other geometric shapes. Its presence in the 2πr squared formula highlights the connection between circles and spheres, as the surface area calculation fundamentally relies on circular dimensions.
-
r (Radius): The radius of a sphere (or hemisphere) is the distance from the center of the sphere to any point on its surface. It is a fundamental measurement that defines the size of the sphere. In the formula, 'r' is squared (r squared), indicating that the surface area increases proportionally to the square of the radius. This means that even small changes in the radius can result in significant changes in the surface area.
-
Squared: Squaring the radius (r²) means multiplying the radius by itself. This operation is crucial because it reflects how the surface area scales with the size of the sphere. The surface area is not directly proportional to the radius but rather to the square of the radius, which is a key geometric property.
-
2πr Squared: This entire expression calculates the surface area of a hemisphere, including the circular base. To clarify, a hemisphere is exactly half of a sphere. When we consider the surface area, it includes the curved surface (like the rounded part of a dome) and the flat, circular base. The formula accounts for both these parts, providing a complete measure of the hemisphere's surface.
The number '2' in the formula makes it specific to the hemisphere. A full sphere's surface area is given by 4πr squared. So, 2πr squared is precisely half of that, plus the area of the circular base (πr squared), together giving the total surface area of the solid hemisphere.
Consider the journey of discovering and formalizing this formula. Ancient mathematicians grappled with understanding curved surfaces long before modern notation existed. Early estimations relied on approximations and geometric dissections. For instance, Archimedes, one of the greatest mathematicians of antiquity, made significant contributions to understanding the surface area of spheres. He demonstrated that the surface area of a sphere is four times the area of its greatest circle (the circle with the same radius as the sphere).
Over centuries, mathematicians refined these ideas, developing more accurate and elegant methods. The introduction of symbolic algebra and calculus provided powerful tools for expressing and proving geometric relationships. The formula 2πr squared, as we know it today, is a product of this rich historical development, representing the culmination of centuries of mathematical exploration and refinement.
Understanding the formula also relies on visualizing and conceptually manipulating shapes in space. Imagine taking a flat circle and gradually curving it into a dome shape. As you curve the circle, you are essentially creating a hemisphere. The formula 2πr squared quantifies the amount of material needed to cover both the curved surface and the circular base of this shape. This mental exercise helps solidify the connection between flat geometry (circles) and three-dimensional geometry (spheres and hemispheres).
Trends and Latest Developments
While the formula 2πr squared itself is a well-established mathematical concept, its application and relevance continue to evolve with advancements in various fields:
-
Materials Science: In materials science, understanding surface area is crucial for designing and analyzing materials with specific properties. For example, the surface area of nanoparticles (tiny particles with diameters on the scale of nanometers) significantly affects their reactivity, catalytic activity, and interaction with other materials. Researchers use variations of the 2πr squared formula, along with sophisticated computational models, to optimize the surface area of nanoparticles for applications ranging from drug delivery to solar energy conversion.
-
Engineering: Engineers use surface area calculations in a wide range of applications, from designing heat exchangers to optimizing the aerodynamics of vehicles. In heat exchangers, a larger surface area allows for more efficient heat transfer between fluids. In aerodynamics, minimizing the surface area of a vehicle can reduce drag and improve fuel efficiency. The 2πr squared formula, along with more complex geometric models, helps engineers make informed design decisions.
-
Environmental Science: Surface area calculations are also essential in environmental science, particularly in studies related to climate change and pollution. For example, the surface area of aerosols (tiny particles suspended in the atmosphere) affects their ability to scatter and absorb sunlight, influencing Earth's radiative balance. Understanding the surface area of these particles is crucial for developing accurate climate models and predicting the impact of pollution on the environment.
-
Medical Field: In medicine, surface area calculations are used to estimate drug dosages, assess burn severity, and analyze the structure of biological tissues. For example, the body surface area (BSA) is often used to calculate the appropriate dose of chemotherapy drugs. The 2πr squared formula, adapted for complex shapes, can also be used to analyze the surface area of cells and tissues, providing insights into their function and health.
-
Data Analysis and Modeling: With the rise of big data and computational modeling, there is an increasing emphasis on accurately representing and analyzing complex shapes. The 2πr squared formula serves as a fundamental building block in many of these models, providing a way to estimate surface areas and related properties. Researchers are developing new algorithms and techniques to efficiently calculate surface areas of complex objects from large datasets, enabling new discoveries in fields ranging from materials science to biology.
The ongoing developments reflect a broader trend towards integrating mathematical models with real-world data to solve complex problems. The 2πr squared formula, while simple in its form, plays a critical role in this process, providing a foundation for understanding and interacting with the physical world.
Tips and Expert Advice
Using the formula 2πr squared effectively requires more than just memorizing it. Here are some practical tips and expert advice to help you apply it accurately and meaningfully:
-
Understand the Context: Before applying the formula, make sure you understand the context of the problem. Are you dealing with a perfect hemisphere, or is the shape slightly different? Knowing the context will help you determine if the formula is appropriate and whether any adjustments are needed. If the object isn't a perfect hemisphere, consider using more advanced techniques like integral calculus to find its surface area.
-
Accurate Measurements: The accuracy of your result depends on the accuracy of your measurements. Use precise instruments to measure the radius of the sphere or hemisphere. If the radius is not uniform, take multiple measurements and calculate an average. For complex shapes, consider using 3D scanning or other advanced techniques to obtain accurate measurements.
-
Units of Measurement: Pay close attention to the units of measurement. Ensure that all measurements are in the same units (e.g., meters, centimeters, inches) before applying the formula. The resulting surface area will be in square units (e.g., square meters, square centimeters, square inches). Always include the units in your final answer to avoid confusion.
-
Estimation and Verification: Before calculating the surface area, make an estimate. This will help you catch any obvious errors in your calculations. After calculating the surface area, verify your result using a different method or by comparing it to known values. For example, you can use online calculators or software tools to check your answer.
-
Real-World Applications: To deepen your understanding, try applying the formula to real-world problems. For example, calculate the amount of paint needed to coat a dome-shaped roof or the amount of fabric required to make a hemispherical tent. This will help you appreciate the practical significance of the formula and improve your problem-solving skills.
Another valuable piece of advice is to visualize the problem geometrically. Draw diagrams or create physical models to help you understand the shape and its dimensions. This can be particularly helpful when dealing with complex shapes or problems that involve multiple steps. By visualizing the problem, you can gain a better intuition for the solution and avoid common mistakes.
Consider the impact of precision in real-world scenarios. Imagine you are an architect designing a geodesic dome. The accuracy of your surface area calculations directly affects the amount of material needed to construct the dome. Even small errors can lead to significant cost overruns or structural problems. Therefore, it is crucial to use precise measurements and calculations, and to double-check your work.
Similarly, in the manufacturing industry, accurate surface area calculations are essential for quality control and cost optimization. For example, if you are producing spherical containers, you need to ensure that each container has the correct surface area to meet customer specifications. By using precise measurements and calculations, you can minimize waste and ensure the quality of your products.
FAQ
-
What is the difference between 2πr squared and πr squared?
- πr squared calculates the area of a circle. 2πr squared calculates the surface area of a hemisphere, including its circular base.
-
Why is the radius squared in the formula?
- Squaring the radius (r²) reflects how the surface area scales with the size of the sphere. The surface area is proportional to the square of the radius, not the radius itself.
-
Can I use this formula for any curved surface?
- No, this formula is specifically for hemispheres. For other curved surfaces, you may need to use more advanced techniques like integral calculus.
-
What are some common mistakes to avoid when using this formula?
- Common mistakes include using the diameter instead of the radius, forgetting to include the correct units of measurement, and applying the formula to shapes that are not hemispheres.
-
Is 2πr squared the same as the lateral surface area of a hemisphere?
- No, it is not. The lateral surface area refers only to the curved surface, without the circular base. That area would be 2πr squared. The formula 2πr squared as a whole gives the total surface area of the solid hemisphere (curved surface plus base).
Conclusion
Understanding the formula 2πr squared goes beyond mere memorization; it involves grasping fundamental geometric principles and appreciating its practical applications. This formula, representing the surface area of a hemisphere, is a powerful tool in various fields, including engineering, materials science, and environmental science. By understanding each component of the formula and its underlying assumptions, we can use it effectively to solve real-world problems.
Whether you're calculating the amount of paint needed for a dome or estimating the surface area of nanoparticles, the principles behind 2πr squared remain essential. To deepen your understanding, try applying these concepts to real-world scenarios and exploring advanced techniques for analyzing complex shapes. Continue exploring the world of mathematics, and you'll discover even more connections between abstract concepts and tangible realities. Want to take the next step in mastering geometry? Share your own experiences with surface area calculations or ask a question in the comments below!
Latest Posts
Latest Posts
-
Is Neptune Bigger Or Smaller Than Earth
Nov 27, 2025
-
How Do You Build A Gable Roof
Nov 27, 2025
-
The Lion The Witch And The Wardrobe Synopsis
Nov 27, 2025
-
How Many Cups Equal 1 4 Pound
Nov 27, 2025
-
Do Private Colleges Receive Federal Funding
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Pi R Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.