Whats The Square Root Of -4
sonusaeterna
Nov 16, 2025 · 11 min read
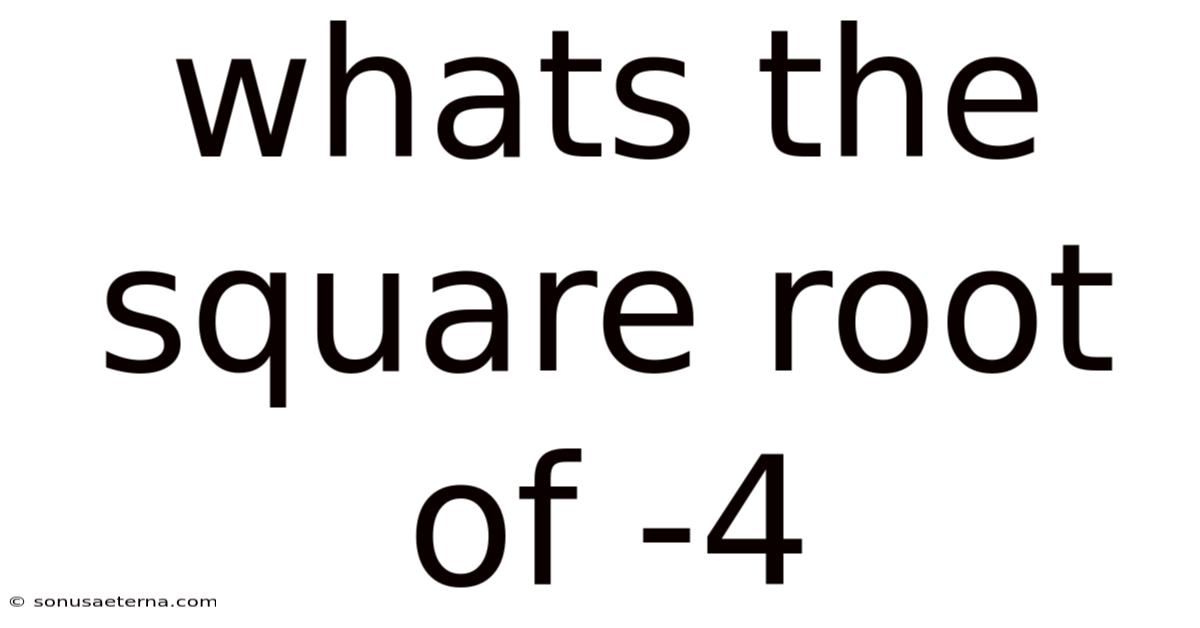
Table of Contents
The question "What's the square root of -4?" often leads to raised eyebrows and the frustrating realization that something’s amiss. We’re taught early on that you can’t take the square root of a negative number. After all, no real number multiplied by itself will ever give you a negative result. But what if I told you that there is an answer, it just exists in a different realm of numbers? Buckle up, because we’re about to dive into the fascinating world of imaginary and complex numbers.
The seemingly simple question opens a gateway to understanding a fundamental concept in mathematics: the existence of numbers beyond what we typically encounter in everyday life. Understanding the square root of -4 requires us to venture into the realm of imaginary numbers, which are crucial in various fields like electrical engineering, quantum mechanics, and advanced physics. This journey will not only provide a solution but will also broaden your perspective on the landscape of mathematics, showing how it adapts and expands to solve previously unsolvable problems.
Unveiling the Mystery: The Square Root of Negative Numbers
To truly appreciate the square root of -4, we need to understand the context in which it exists. We must explore the concept of imaginary numbers and how they fit into the broader structure of complex numbers. Why do we even need these "imaginary" numbers in the first place? What problems do they solve, and how do they help us understand the world around us?
Let’s start with the basics. A square root of a number x is a value that, when multiplied by itself, gives you x. For example, the square root of 9 is 3 because 3 * 3 = 9. Similarly, the square root of 25 is 5 because 5 * 5 = 25. These are all real numbers. But what happens when we try to find the square root of a negative number, like -1?
The problem here is that no real number, when multiplied by itself, can give you a negative number. A positive number multiplied by a positive number is always positive. A negative number multiplied by a negative number is also positive (because a negative times a negative equals a positive). Therefore, the square root of a negative number cannot be a real number. This is where imaginary numbers come into play.
Comprehensive Overview of Imaginary and Complex Numbers
The concept of imaginary numbers was first introduced in the 16th century by mathematicians grappling with equations that had no real solutions. The Italian mathematician Gerolamo Cardano was one of the first to work with imaginary numbers, though he considered them more of a mathematical curiosity than a practical tool. It wasn't until later that mathematicians began to understand their true potential.
The foundation of imaginary numbers is the imaginary unit, denoted as i. By definition, i is the square root of -1. In other words:
i = √-1
This simple definition opens up a whole new world of possibilities. With i in our toolkit, we can now express the square root of any negative number. For example, the square root of -9 can be written as:
√-9 = √(9 * -1) = √9 * √-1 = 3i
So, the square root of -9 is 3i, which is an imaginary number. An imaginary number is simply a real number multiplied by the imaginary unit i.
Now, let’s get back to the original question: What is the square root of -4? Using the same logic:
√-4 = √(4 * -1) = √4 * √-1 = 2i
Therefore, the square root of -4 is 2i.
But imaginary numbers don't exist in isolation. They are part of a larger system called complex numbers. A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit. In this form:
- a is called the real part of the complex number.
- b is called the imaginary part of the complex number.
For example, 3 + 2i is a complex number where 3 is the real part and 2 is the imaginary part. Complex numbers encompass both real numbers (when b = 0) and imaginary numbers (when a = 0). This makes them a comprehensive system for handling a wide range of mathematical problems.
Complex numbers can be visualized on a complex plane, which is similar to a Cartesian plane but with the horizontal axis representing the real part and the vertical axis representing the imaginary part. A complex number a + bi can be plotted as a point (a, b) on this plane. This graphical representation makes it easier to understand the properties and operations of complex numbers, such as addition, subtraction, multiplication, and division.
The introduction of complex numbers wasn't just a theoretical exercise. It allowed mathematicians and scientists to solve problems that were previously unsolvable using only real numbers. For instance, complex numbers are essential in solving certain types of algebraic equations, particularly cubic equations, which often have complex roots.
Trends and Latest Developments in Complex Numbers
Today, complex numbers are not just a mathematical curiosity but a fundamental tool in many areas of science and engineering. They play a crucial role in:
- Electrical Engineering: Analyzing alternating current (AC) circuits. The impedance (resistance to AC) is represented as a complex number, allowing engineers to easily calculate voltage and current in complex circuits.
- Quantum Mechanics: Describing the behavior of particles at the atomic and subatomic levels. Wave functions, which describe the probability of finding a particle in a particular state, are complex-valued.
- Fluid Dynamics: Modeling fluid flow. Complex potentials are used to simplify calculations of velocity and pressure fields in two-dimensional fluid flows.
- Signal Processing: Analyzing and manipulating signals. Fourier transforms, which are used to decompose signals into their constituent frequencies, rely heavily on complex numbers.
- Control Systems: Designing and analyzing systems that regulate the behavior of dynamic systems. Complex numbers are used to analyze the stability and performance of control systems.
Recent developments in these fields continue to rely on complex numbers. For example, in quantum computing, qubits (quantum bits) are represented as complex vectors, allowing for computations that are impossible with classical bits. In electrical engineering, advanced signal processing techniques use complex numbers to filter noise and extract information from noisy signals.
The use of complex numbers is also expanding into new areas. For example, in image processing, complex wavelets are used to analyze and enhance images. In finance, complex numbers are used to model financial markets and analyze investment strategies. The ongoing research and development in these areas ensure that complex numbers will remain a vital tool for scientists and engineers for many years to come.
Moreover, there's a growing trend in educational approaches to introduce complex numbers earlier in the mathematics curriculum. By exposing students to these concepts sooner, educators aim to foster a deeper understanding of mathematical principles and better prepare them for advanced studies in science and engineering. This shift reflects the increasing importance of complex numbers in modern technology and research.
Tips and Expert Advice for Mastering Complex Numbers
Understanding and working with complex numbers can be challenging, but with the right approach, anyone can master them. Here are some practical tips and expert advice to help you on your journey:
-
Start with the Basics: Ensure you have a solid understanding of real numbers, algebraic operations, and basic geometry. Complex numbers build upon these fundamental concepts, so a strong foundation is essential. Spend time reviewing these topics if necessary.
-
Visualize Complex Numbers: Use the complex plane to visualize complex numbers. Plotting numbers on the plane can help you understand their magnitude and direction. This is particularly useful when performing operations like addition and multiplication, as it provides a geometric interpretation of these operations.
-
Practice, Practice, Practice: The more you work with complex numbers, the more comfortable you will become. Solve a variety of problems involving addition, subtraction, multiplication, division, and exponentiation of complex numbers. Look for patterns and shortcuts to improve your problem-solving skills.
-
Use Online Resources: There are many excellent online resources available to help you learn about complex numbers. Websites like Khan Academy, Wolfram Alpha, and various university math departments offer tutorials, examples, and practice problems. Take advantage of these resources to supplement your learning.
-
Understand Euler's Formula: Euler's formula (e^iθ = cos θ + i sin θ) is a fundamental result that connects complex numbers to trigonometry and exponential functions. Understanding this formula is crucial for many applications of complex numbers, such as analyzing AC circuits and solving differential equations.
-
Learn to Convert Between Forms: Complex numbers can be represented in rectangular form (a + bi) and polar form (r(cos θ + i sin θ)). Being able to convert between these forms is essential for simplifying calculations and understanding the geometric properties of complex numbers.
-
Apply Complex Numbers to Real-World Problems: One of the best ways to understand complex numbers is to see how they are used in real-world applications. Explore how complex numbers are used in electrical engineering, quantum mechanics, and other fields. This will give you a deeper appreciation for their power and versatility.
-
Don't Be Afraid to Ask for Help: If you're struggling with complex numbers, don't hesitate to ask for help from teachers, professors, or fellow students. Mathematics is often a collaborative endeavor, and discussing your difficulties with others can lead to new insights and a better understanding of the material.
By following these tips and putting in the effort to practice and explore, you can master complex numbers and unlock their potential for solving a wide range of mathematical and scientific problems. Remember, the key is to build a solid foundation, visualize the concepts, and apply them to real-world scenarios.
FAQ About Square Roots and Complex Numbers
Q: Why can't you take the square root of a negative number in the real number system?
A: Because any real number multiplied by itself will always result in a non-negative number. A positive times a positive is positive, and a negative times a negative is also positive.
Q: What is the imaginary unit i?
A: The imaginary unit i is defined as the square root of -1, i.e., i = √-1.
Q: What is a complex number?
A: A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit. a is the real part, and b is the imaginary part.
Q: Can a real number be a complex number?
A: Yes, a real number can be considered a complex number where the imaginary part is zero. For example, the real number 5 can be written as the complex number 5 + 0i.
Q: How do you add or subtract complex numbers?
A: To add complex numbers, add the real parts and the imaginary parts separately. For example, (3 + 2i) + (1 - i) = (3 + 1) + (2 - 1)i = 4 + i. Subtraction is similar: (3 + 2i) - (1 - i) = (3 - 1) + (2 + 1)i = 2 + 3i.
Q: How do you multiply complex numbers?
A: To multiply complex numbers, use the distributive property and remember that i² = -1. For example, (2 + i) * (3 - 2i) = 23 + 2(-2i) + i3 + i(-2i) = 6 - 4i + 3i - 2i² = 6 - i + 2 = 8 - i.
Q: What are some real-world applications of complex numbers?
A: Complex numbers are used in various fields, including electrical engineering (analyzing AC circuits), quantum mechanics (describing wave functions), fluid dynamics (modeling fluid flow), and signal processing (analyzing signals).
Q: What is the complex conjugate of a complex number?
A: The complex conjugate of a complex number a + bi is a - bi. It is obtained by changing the sign of the imaginary part.
Conclusion
So, what have we learned? The square root of -4 is not a real number, but it is a valid number within the realm of complex numbers. Specifically, √-4 = 2i, where i is the imaginary unit, defined as the square root of -1. This exploration has taken us beyond the familiar territory of real numbers into the fascinating world of imaginary and complex numbers, which are essential tools in many scientific and engineering disciplines.
Complex numbers are not just abstract mathematical concepts; they are powerful tools that help us solve real-world problems. From analyzing AC circuits in electrical engineering to describing the behavior of particles in quantum mechanics, complex numbers play a crucial role in our understanding of the world. By embracing these concepts and developing a solid understanding of their properties, you can unlock new possibilities and expand your problem-solving abilities.
Now that you understand the basics, take the next step. Explore more complex problems, delve into the applications of complex numbers in your field of interest, and continue to expand your mathematical horizons. Share this article with others who might be curious about the square root of negative numbers and invite them to join the journey of mathematical discovery. Leave a comment below with your thoughts or questions about complex numbers. What other mathematical mysteries would you like to explore?
Latest Posts
Latest Posts
-
Books By Maya Angelou In Order
Nov 17, 2025
-
What Is Language Translator In Computer
Nov 17, 2025
-
Dividing And Multiplying Negative And Positive Numbers
Nov 17, 2025
-
When To Use The Em Dash
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of -4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.