What Percentage Of 100 Is 50
sonusaeterna
Nov 19, 2025 · 11 min read
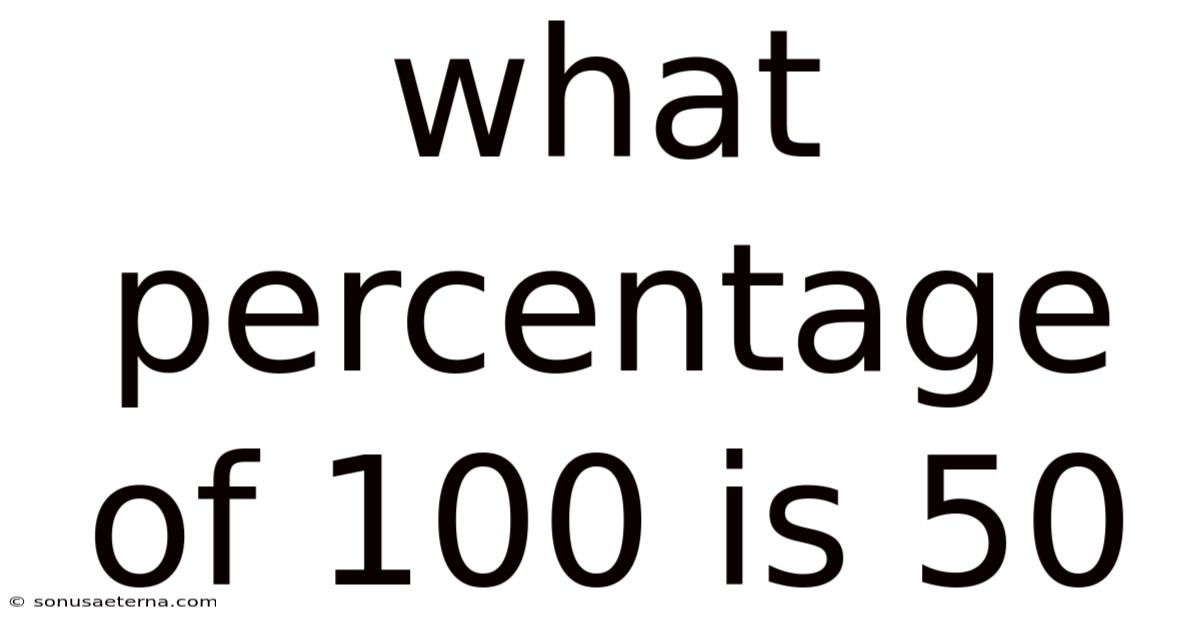
Table of Contents
The question "What percentage of 100 is 50?" might seem simple at first glance, but it’s a fundamental concept that underscores many aspects of mathematics, finance, and everyday life. Understanding percentages is crucial for calculating discounts, understanding statistics, and making informed decisions. This article will delve into the concept of percentages, explore the calculation behind determining what percentage of 100 is 50, and discuss the broader applications of percentages in various contexts.
Understanding the Basics of Percentages
Percentages are a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Percentages are used to express how large one quantity is relative to another quantity. To calculate a percentage, you generally divide the part by the whole and then multiply by 100. This gives you the proportion of the whole that the part represents, expressed as a percentage.
The Formula for Percentage Calculation
The basic formula for calculating a percentage is:
Percentage = (Part / Whole) × 100
In this formula:
- Part is the specific amount you are interested in.
- Whole is the total or reference amount.
- The result is the percentage, which tells you how much of the whole the part represents.
Applying the Formula to "What Percentage of 100 is 50?"
To answer the question "What percentage of 100 is 50?", we can use the formula as follows:
- Part = 50
- Whole = 100
So, the calculation becomes: Percentage = (50 / 100) × 100 Percentage = 0.5 × 100 Percentage = 50%
Therefore, 50 is 50% of 100. This simple calculation illustrates the fundamental principle of percentages.
The Significance of Using 100 as the Base
Using 100 as the base for percentage calculations makes it easy to understand and compare proportions. When the whole is 100, the percentage is simply the same as the part. This is why understanding percentages with 100 as the base is so straightforward. For example, if you score 80 out of 100 on a test, your score is immediately understandable as 80%.
History and Evolution of Percentages
The use of percentages dates back to ancient Rome, where taxes were often calculated as fractions of assets. However, the modern concept of percentage became more prevalent in Europe during the 15th century, with the growth of arithmetic and commerce. The symbol "%" evolved over time from various notations used to represent "per cento" or "per centum." The standardization of percentages has made it an indispensable tool in various fields, from finance to statistics.
The Role of Percentages in Different Fields
Percentages play a crucial role in numerous fields:
- Finance: Used to calculate interest rates, investment returns, and inflation rates.
- Statistics: Used to express data in a standardized way, making it easier to compare different datasets.
- Retail: Used to calculate discounts, sales tax, and profit margins.
- Education: Used to grade exams and assess student performance.
- Health: Used to express probabilities and risks, such as the success rate of a medical treatment.
Comprehensive Overview of Percentage Applications
Percentages are not just abstract mathematical concepts; they are practical tools that help us understand and interpret the world around us. Understanding how percentages are used in different fields can provide valuable insights and improve decision-making.
Financial Applications of Percentages
In finance, percentages are used extensively to calculate returns on investments. For example, if you invest $1,000 in a stock and it grows to $1,100 in a year, the return on your investment is:
Return = (($1,100 - $1,000) / $1,000) × 100 Return = ($100 / $1,000) × 100 Return = 10%
This means your investment grew by 10% over the year.
Interest Rates: Interest rates, whether on loans or savings accounts, are expressed as percentages. An interest rate of 5% on a savings account means that you will earn 5% of your account balance each year. Inflation Rates: Inflation rates are also expressed as percentages and indicate how much the prices of goods and services have increased over a period, typically a year.
Statistical Applications of Percentages
In statistics, percentages are used to summarize and compare data. For instance, if a survey finds that 600 out of 1,000 people prefer a particular brand of coffee, this can be expressed as 60%.
Data Representation: Percentages make it easier to understand the distribution of data and compare different groups. For example, if you want to compare the proportion of male and female employees in a company, expressing the numbers as percentages can provide a clearer picture. Margin of Error: In surveys, the margin of error is often expressed as a percentage, indicating the range within which the true population value is likely to fall.
Retail Applications of Percentages
Retail businesses use percentages to manage pricing, discounts, and profitability.
Discounts: Discounts are commonly expressed as percentages. A 20% discount on an item that costs $50 means that the price is reduced by 20% of $50, which is $10. The new price is $50 - $10 = $40. Profit Margins: Profit margins are also expressed as percentages, indicating the proportion of revenue that remains after deducting the costs of goods sold. A profit margin of 30% means that for every dollar of revenue, the company makes 30 cents in profit.
Educational Applications of Percentages
In education, percentages are used to evaluate student performance and track academic progress.
Grading: Test scores are often converted to percentages to provide a standardized measure of performance. A score of 75 out of 100 on a test is easily understood as 75%. Ranking: Percentiles are used to rank students relative to their peers. A student who scores in the 90th percentile has performed better than 90% of the other students.
Health Applications of Percentages
In healthcare, percentages are used to communicate risks, success rates, and other important information.
Survival Rates: Survival rates for diseases are often expressed as percentages. For example, a 5-year survival rate of 80% for a particular type of cancer means that 80% of patients with that cancer are still alive five years after diagnosis. Vaccination Rates: Vaccination rates are also expressed as percentages, indicating the proportion of the population that has been vaccinated against a particular disease.
Trends and Latest Developments in Percentage Usage
The way percentages are used continues to evolve with advancements in technology and data analysis. Here are some current trends and developments:
Data Visualization
Percentages are increasingly being used in data visualization to make complex information more accessible. Charts and graphs often use percentages to represent proportions and distributions, allowing viewers to quickly grasp key insights.
Machine Learning and AI
In the field of machine learning, percentages are used to evaluate the performance of algorithms. Accuracy, precision, and recall are often expressed as percentages to measure how well a model is performing. For example, an algorithm with an accuracy of 95% correctly classifies 95% of the data points.
E-commerce and Digital Marketing
E-commerce platforms use percentages to track conversion rates, click-through rates, and other key performance indicators (KPIs). These metrics help businesses optimize their marketing efforts and improve sales.
Public Health and Policy
During the COVID-19 pandemic, percentages were used extensively to track infection rates, vaccination rates, and mortality rates. This information helped policymakers make informed decisions about public health interventions.
Professional Insights
As data becomes more readily available, the ability to interpret and communicate percentages effectively is becoming increasingly important. Professionals in various fields need to be able to understand percentages, calculate them accurately, and present them in a way that is easy for others to understand. This includes not only technical skills but also the ability to contextualize the data and explain its significance.
Tips and Expert Advice for Working with Percentages
Working with percentages can be straightforward, but it's essential to follow some best practices to ensure accuracy and clarity.
Double-Check Your Calculations
One of the most important tips for working with percentages is to double-check your calculations. It's easy to make mistakes, especially when dealing with complex calculations. Use a calculator or spreadsheet to verify your results.
Example: Suppose you are calculating a 15% tip on a $45 bill. A quick way to estimate is to find 10% of $45, which is $4.50, and then add half of that amount ($2.25) to get $6.75. Always verify this with a calculator to ensure accuracy.
Understand the Base
When interpreting percentages, it's crucial to understand the base or reference amount. A small percentage change can be significant if the base is very large, and vice versa.
Example: A 1% increase in the population of a small town might only mean a few additional people, while a 1% increase in the population of a large city could mean thousands of new residents.
Avoid Percentage of Percentage Errors
One common mistake is to calculate a percentage of a percentage incorrectly. For example, if an item is discounted by 20% and then an additional 10%, the total discount is not 30%.
Example: If an item costs $100 and is discounted by 20%, the new price is $80. If it is then discounted by an additional 10%, the new price is 90% of $80, which is $72. The total discount is $28, or 28%, not 30%.
Use Percentages to Compare Proportions
Percentages are most useful when comparing proportions. They provide a standardized way to compare different groups or datasets, even if the total numbers are different.
Example: If you want to compare the proportion of students who passed a test in two different classes, it's more informative to compare the percentages of students who passed rather than the absolute numbers.
Communicate Percentages Clearly
When presenting percentages, it's essential to communicate them clearly and avoid ambiguity. Use clear language and provide context to help your audience understand the significance of the numbers.
Example: Instead of saying "Sales increased by 5%," you could say "Sales increased by 5% compared to the same period last year, indicating strong growth."
Round Appropriately
When presenting percentages, it's often necessary to round the numbers to make them easier to understand. However, be careful not to round too much, as this can distort the data.
Example: If a calculation results in 75.567%, rounding to 75.6% or 76% may be appropriate, depending on the context. Rounding to 80% would be too much and could mislead the audience.
Use Visual Aids
Visual aids such as charts and graphs can be very effective for communicating percentages. Use pie charts to show proportions, bar graphs to compare different groups, and line graphs to track changes over time.
FAQ About Percentages
Q: How do I convert a fraction to a percentage? A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply by 100. For example, to convert 3/4 to a percentage, calculate (3 / 4) × 100 = 75%.
Q: How do I convert a decimal to a percentage? A: To convert a decimal to a percentage, multiply the decimal by 100. For example, to convert 0.65 to a percentage, calculate 0.65 × 100 = 65%.
Q: How do I calculate a percentage increase or decrease? A: To calculate a percentage increase or decrease, use the formula: ((New Value - Old Value) / Old Value) × 100. If the result is positive, it's an increase; if it's negative, it's a decrease.
Q: What is the difference between percentage and percentile? A: Percentage represents a proportion out of 100, while percentile represents the value below which a given percentage of observations in a group of observations falls. For example, a score in the 80th percentile means that the score is higher than 80% of the other scores.
Q: How do I calculate a percentage of a number? A: To calculate a percentage of a number, multiply the number by the percentage expressed as a decimal. For example, to calculate 20% of 500, calculate 0.20 × 500 = 100.
Conclusion
Understanding that 50 is 50 percent of 100 is a foundational concept that simplifies more complex percentage calculations and applications. Percentages are a ubiquitous tool in finance, statistics, retail, education, and health, enabling us to make informed decisions and interpret data effectively. By grasping the basics of percentage calculations, understanding their various applications, and following best practices, you can enhance your analytical skills and improve your ability to navigate the world around you. Ready to put your knowledge to the test? Try calculating some percentages in your daily life, whether it's figuring out a tip at a restaurant or understanding the discount on a sale item. Engage with percentages to truly master them.
Latest Posts
Latest Posts
-
How Long Is Bridge To Florida Keys
Nov 19, 2025
-
What River Was The Three Gorges Dam Built On
Nov 19, 2025
-
Dermatomal Maps Are Important Clinically Because They
Nov 19, 2025
-
What Is Dhppv Vaccine For Dogs
Nov 19, 2025
-
Square Root Of X Square Root Of X
Nov 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 100 Is 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.