What Is Half Of 3 4 C
sonusaeterna
Nov 16, 2025 · 11 min read
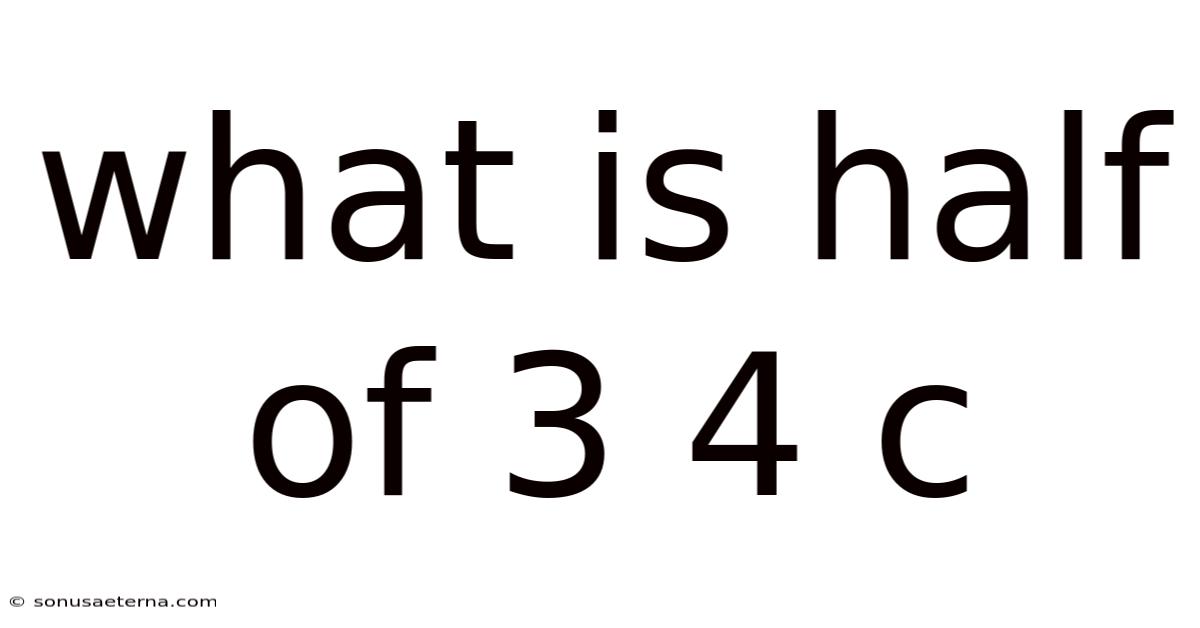
Table of Contents
Imagine you are in a bustling kitchen, apron on, ready to bake your grandmother’s famous chocolate chip cookies. The recipe calls for "3/4 cup of sugar," but you only want to make half a batch. Suddenly, a simple baking session turns into a math problem. What exactly is half of 3/4 cup? This scenario highlights how fractions, like 3/4, frequently appear in everyday contexts, from cooking and crafting to construction and finance.
Understanding how to find half of a fraction is a fundamental skill that empowers you to tackle real-world situations with confidence. It’s not just about crunching numbers; it's about gaining a deeper understanding of proportions and ratios, enabling you to make informed decisions and solve problems efficiently. In this article, we will unravel the mystery behind finding half of 3/4, exploring various methods and providing practical examples to solidify your understanding.
Understanding Fractions: A Foundation for Calculation
Before diving into the specific calculation of half of 3/4, it's essential to have a solid understanding of what fractions represent. A fraction is a way of representing a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number), separated by a line. The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
In the fraction 3/4, the denominator, 4, tells us that the whole is divided into four equal parts. The numerator, 3, tells us that we are considering three of those four parts. This can be visualized as a pie cut into four equal slices, where you have three of those slices. Understanding this fundamental concept is crucial for grasping how to manipulate and calculate with fractions.
Fractions can represent various things, such as parts of a physical object (like the pie example), ratios between quantities, or even probabilities. They are a fundamental building block of mathematics and are used extensively in various fields, from engineering and physics to finance and economics. Being comfortable with fractions is, therefore, an essential skill for both academic and practical purposes.
The Language of Fractions: Numerator and Denominator
As we've established, the numerator and denominator are the key components of a fraction. The numerator represents the specific number of parts you have, while the denominator indicates the total number of equal parts that make up the whole. Think of it like this: the denominator "nominates" the type of part you're dealing with (fourths, fifths, tenths, etc.), and the numerator tells you how many of those nominated parts you possess.
Understanding the relationship between the numerator and denominator is essential for performing operations on fractions, such as addition, subtraction, multiplication, and division. For example, when adding fractions, you need to ensure they have the same denominator before you can add the numerators. Similarly, when comparing fractions, understanding the relative size of the numerator and denominator helps you determine which fraction represents a larger portion of the whole.
Equivalent Fractions: Different Faces, Same Value
Equivalent fractions are different fractions that represent the same value. For example, 1/2, 2/4, and 4/8 are all equivalent fractions. They all represent the same portion of a whole. This concept is essential for simplifying fractions and performing operations with fractions that have different denominators.
Finding equivalent fractions involves multiplying or dividing both the numerator and denominator by the same non-zero number. For example, to find an equivalent fraction for 1/2 with a denominator of 4, you would multiply both the numerator and denominator by 2, resulting in 2/4. Understanding equivalent fractions allows you to manipulate fractions without changing their underlying value, which is crucial for solving many mathematical problems.
Mixed Numbers and Improper Fractions
Fractions can also be represented as mixed numbers or improper fractions. A mixed number consists of a whole number and a proper fraction (a fraction where the numerator is less than the denominator). For example, 1 1/2 is a mixed number representing one whole and one-half. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. For example, 3/2 is an improper fraction representing one and one-half.
It's often necessary to convert between mixed numbers and improper fractions when performing calculations. To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, to convert 1 1/2 to an improper fraction, you would (1 * 2) + 1 = 3, resulting in 3/2. To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient is the whole number, and the remainder is the numerator of the fractional part, with the same denominator.
Finding Half of 3/4: Methods and Explanations
Now that we have a strong foundation in fractions, let's explore how to find half of 3/4. There are several methods you can use, each offering a slightly different perspective on the problem. We'll cover the most common and intuitive approaches.
Method 1: Dividing by 2
The most straightforward approach is to directly divide the fraction 3/4 by 2. Remember that dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 2 (or 2/1) is 1/2. Therefore, finding half of 3/4 is the same as multiplying 3/4 by 1/2.
To multiply fractions, you simply multiply the numerators together and the denominators together. So, (3/4) * (1/2) = (3 * 1) / (4 * 2) = 3/8. Therefore, half of 3/4 is 3/8. This method is quick and efficient, especially when you're comfortable with fraction multiplication.
Method 2: Visual Representation
Another helpful way to understand finding half of 3/4 is to use a visual representation. Imagine a rectangle divided into four equal parts, representing the denominator of 4. Shade three of those parts to represent the numerator of 3. You now have a visual representation of 3/4.
To find half of this, imagine dividing each of the four parts in half. This now gives you eight equal parts in total. The three shaded parts, which originally represented 3/4, now represent six of those eight parts. However, you only want half of the original 3/4, so you need to take half of the shaded area. Visually, this would mean selecting three of the eight parts. Therefore, half of 3/4 is visually represented as 3/8. This method is particularly helpful for visual learners and can make the concept more concrete.
Method 3: Converting to Decimals
Fractions can also be converted to decimals, which can sometimes simplify calculations. To convert 3/4 to a decimal, you divide the numerator (3) by the denominator (4). This gives you 0.75. Now, to find half of 0.75, you simply divide 0.75 by 2, which results in 0.375.
To convert 0.375 back to a fraction, you can recognize that 0.375 is equivalent to 375/1000. This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 125. This results in 3/8. Therefore, half of 3/4, expressed as a decimal, is 0.375, which is equivalent to the fraction 3/8. This method can be useful if you're more comfortable working with decimals than fractions.
Practical Applications: Where Does This Matter?
Understanding how to find half of 3/4 isn't just an abstract mathematical exercise. It has numerous practical applications in everyday life. Here are a few examples:
- Cooking and Baking: As illustrated in the opening scenario, recipes often call for fractional amounts of ingredients. If you want to halve a recipe that calls for 3/4 cup of flour, you need to know that half of 3/4 is 3/8, meaning you'll need 3/8 cup of flour.
- Construction and DIY Projects: When working on home improvement projects, you might need to cut materials to specific sizes. If a piece of wood needs to be 3/4 of a meter long, and you need to cut it in half, you'll need to know that half of 3/4 is 3/8 of a meter.
- Sharing and Dividing: Imagine you have 3/4 of a pizza left, and you want to share it equally with a friend. You would need to divide the pizza in half, resulting in each of you getting 3/8 of the whole pizza.
- Finance and Percentages: Understanding fractions is crucial for understanding percentages, which are widely used in finance. For example, if an item is 3/4 of its original price, and you get an additional 50% off (which is half), you need to calculate half of 3/4 to determine the final discount.
These are just a few examples, but they illustrate how understanding fractions and knowing how to find half of a fraction is a valuable skill in various real-world scenarios.
Tips and Expert Advice
Here are some helpful tips and expert advice to master finding half of 3/4 and working with fractions in general:
- Visualize Fractions: Use diagrams, drawings, or physical objects to visualize fractions. This can make the concept more concrete and easier to understand. Imagine cutting a pie or dividing a rectangle into equal parts to represent the fraction.
- Practice Regularly: The more you practice working with fractions, the more comfortable you'll become. Try solving various problems involving fractions, including finding halves, quarters, and other fractions of fractions.
- Simplify Fractions: Always try to simplify fractions to their lowest terms. This makes calculations easier and helps you better understand the relationship between the numerator and denominator.
- Use Equivalent Fractions: When adding or subtracting fractions with different denominators, find equivalent fractions with a common denominator. This allows you to perform the operations easily.
- Convert to Decimals (If Helpful): If you find it easier to work with decimals, convert the fractions to decimals before performing calculations. However, be aware that some fractions may result in repeating decimals, which can make calculations more complex.
- Double-Check Your Work: Always double-check your work to ensure you haven't made any errors. This is especially important when dealing with fractions, as errors can easily occur.
- Use Online Resources: There are many online resources available to help you learn and practice fractions, including tutorials, quizzes, and calculators. Utilize these resources to reinforce your understanding.
- Relate to Real-World Examples: Try to relate fractions to real-world examples to make the concept more relevant and engaging. This can help you see the practical applications of fractions and motivate you to learn more.
- Don't Be Afraid to Ask for Help: If you're struggling with fractions, don't be afraid to ask for help from a teacher, tutor, or friend. Everyone learns at their own pace, and there's no shame in seeking assistance.
- Master Multiplication and Division: Strong multiplication and division skills are essential for working with fractions. Ensure you have a solid understanding of these operations before tackling more complex fraction problems.
FAQ
Q: What is a fraction?
A: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number), separated by a line. The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Q: How do I find half of a fraction?
A: You can find half of a fraction by dividing the fraction by 2 (which is the same as multiplying by 1/2) or by converting the fraction to a decimal and dividing the decimal by 2.
Q: What is the reciprocal of a number?
A: The reciprocal of a number is 1 divided by that number. For example, the reciprocal of 2 is 1/2.
Q: How do I multiply fractions?
A: To multiply fractions, you simply multiply the numerators together and the denominators together.
Q: What are equivalent fractions?
A: Equivalent fractions are different fractions that represent the same value. For example, 1/2, 2/4, and 4/8 are all equivalent fractions.
Q: How do I convert a fraction to a decimal?
A: To convert a fraction to a decimal, you divide the numerator by the denominator.
Q: Why are fractions important?
A: Fractions are important because they are used extensively in various fields, from cooking and crafting to construction and finance. Understanding fractions is essential for solving real-world problems and making informed decisions.
Conclusion
Finding half of 3/4 is a fundamental mathematical skill with practical applications in numerous aspects of life. Whether you choose to divide by 2, visualize the fraction, or convert to decimals, understanding the underlying concepts of fractions is key to mastering this calculation. By utilizing the tips and expert advice provided, you can confidently tackle any problem involving fractions and enhance your overall mathematical proficiency.
Now that you've mastered finding half of 3/4, why not put your skills to the test? Try applying this knowledge to a real-world scenario, such as adjusting a recipe or dividing a quantity of materials. Share your experiences and any other helpful tips in the comments below!
Latest Posts
Latest Posts
-
How Many Factors Does 9 Have
Nov 16, 2025
-
What Are The 7 Rights Of Medication Administration
Nov 16, 2025
-
Who Was The Most Powerful Egyptian God
Nov 16, 2025
-
When Can You Use Hyphens In A Sentence
Nov 16, 2025
-
Algebra With X On Both Sides
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3 4 C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.