What Is Five Percent Of 100
sonusaeterna
Nov 20, 2025 · 15 min read
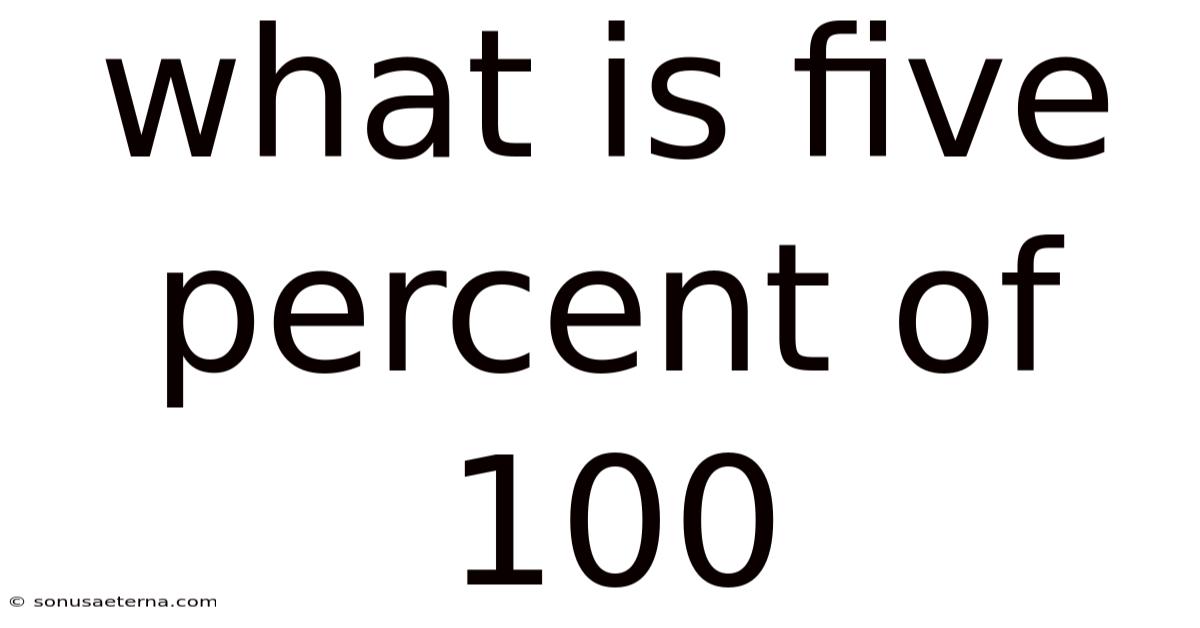
Table of Contents
Have you ever been in a situation where you needed to quickly calculate a discount while shopping, or figure out a tip at a restaurant? These everyday scenarios often require basic percentage calculations. Understanding how to work with percentages can be incredibly useful, saving you time and stress in many situations. In this article, we'll break down a very fundamental example: what is five percent of 100?
Though simple, understanding how to calculate five percent of 100 is a cornerstone for grasping more complex percentage problems. We will explore the concept of percentages, step-by-step methods for calculating them, real-world applications, and practical tips to enhance your understanding. Whether you’re a student looking to improve your math skills or someone wanting to brush up on your basic arithmetic, this guide will provide you with the knowledge and confidence to tackle percentage calculations with ease.
Understanding Percentages: A Comprehensive Overview
Percentages are a fundamental concept in mathematics with widespread applications in various aspects of life. To fully understand what five percent of 100 means, it's essential to first grasp the basics of percentages and their significance.
Definition of Percentage
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." It is denoted by the symbol "%." In essence, a percentage tells you how many parts out of 100 you have. For example, if you have 25%, you have 25 parts out of 100.
Percentages are used to express proportions, ratios, or fractions in a standardized format, making it easier to compare and understand quantities. They are a versatile tool used in finance, statistics, retail, and many other fields.
The Basic Formula
The basic formula to calculate a percentage is:
Percentage = (Part / Whole) × 100
Where:
- Part is the specific quantity you are interested in.
- Whole is the total quantity or the reference value.
To find what percentage a part is of a whole, you divide the part by the whole and then multiply by 100 to express the result as a percentage.
Historical Context
The concept of percentages dates back to ancient Rome. As the Roman Empire expanded, the need for standardized methods of financial calculation grew. The Romans used fractions based on 100 (such as calculating taxes) because it was simple to understand and apply.
However, the modern percentage symbol (%) did not appear until much later. It evolved gradually through the Middle Ages and Renaissance. One theory suggests that the symbol evolved from an Italian abbreviation for per cento – c.to – which was eventually shortened to c/o and then stylized into the % symbol.
Importance of Understanding Percentages
Understanding percentages is crucial for several reasons:
- Financial Literacy: Percentages are widely used in finance to express interest rates, investment returns, and discounts. Knowing how to calculate and interpret percentages helps you make informed financial decisions.
- Data Interpretation: In statistics and data analysis, percentages are used to summarize and compare data sets. Understanding percentages allows you to interpret data accurately and draw meaningful conclusions.
- Everyday Life: From calculating tips at restaurants to understanding sales discounts, percentages are a part of everyday life. Being able to quickly calculate percentages can save you time and money.
- Problem Solving: Percentages are used in various problem-solving scenarios, from determining the percentage increase or decrease in sales to calculating the percentage of students who passed an exam.
Basic Percentage Calculations
Let's look at some basic percentage calculations to illustrate the concept:
- Example 1: Finding a Percentage of a Number
- What is 20% of 50?
- Solution: (20/100) × 50 = 10
- Example 2: Finding What Percentage One Number Is of Another
- What percentage is 15 of 75?
- Solution: (15/75) × 100 = 20%
- Example 3: Increasing a Number by a Percentage
- Increase 100 by 10%.
- Solution: 10% of 100 = 10, so 100 + 10 = 110
- Example 4: Decreasing a Number by a Percentage
- Decrease 200 by 25%.
- Solution: 25% of 200 = 50, so 200 - 50 = 150
Understanding these basic calculations is essential for more complex percentage problems and their applications in real-world scenarios.
Calculating Five Percent of 100: Step-by-Step
Now that we have a solid understanding of percentages, let's focus on calculating five percent of 100. This specific calculation is straightforward, but it provides a clear example of how to apply the percentage formula.
Method 1: Using the Percentage Formula
The most direct way to calculate five percent of 100 is by using the percentage formula:
Percentage = (Part / Whole) × 100
In this case, we want to find the "Part" when the "Whole" is 100 and the "Percentage" is 5%. Rearranging the formula to solve for the "Part":
Part = (Percentage / 100) × Whole
Plugging in the values:
Part = (5 / 100) × 100
Part = 0.05 × 100
Part = 5
So, five percent of 100 is 5.
Method 2: Converting Percentage to Decimal
Another way to calculate five percent of 100 is by converting the percentage to a decimal. To do this, divide the percentage by 100:
5% = 5 / 100 = 0.05
Now, multiply this decimal by the whole number:
- 05 × 100 = 5
Again, we find that five percent of 100 is 5.
Method 3: Using Fractions
Percentages can also be expressed as fractions. Five percent is equivalent to the fraction 5/100, which can be simplified to 1/20. To find five percent of 100, multiply 100 by the fraction:
(1/20) × 100 = 100/20 = 5
This method also shows that five percent of 100 is 5.
Why is Understanding This Calculation Important?
Calculating five percent of 100 might seem simple, but it’s a foundational step in understanding how percentages work. This basic understanding is crucial for:
- Mental Math: Being able to quickly calculate simple percentages like 5% of 100 builds confidence and speed in mental math.
- Real-World Applications: This skill can be applied to various scenarios, such as calculating discounts, tips, or understanding basic financial concepts.
- Building a Foundation: Mastering simple percentage calculations provides a solid foundation for tackling more complex problems in mathematics and finance.
Practical Examples
Let's consider some practical examples where knowing that five percent of 100 is 5 can be useful:
- Simple Interest: If you invest $100 at a 5% simple interest rate per year, you will earn $5 in interest each year.
- Discounts: If an item originally costs $100 and is on sale for 5% off, the discount amount is $5, making the new price $95.
- Budgeting: If you allocate 5% of your $100 weekly budget to entertainment, you have $5 to spend on entertainment.
These examples illustrate how understanding and being able to quickly calculate five percent of 100 can be beneficial in various everyday situations.
Trends and Latest Developments in Percentage Applications
While the basic principles of percentages remain constant, their applications continue to evolve with new trends and developments in various fields. Here’s a look at some of the latest trends and how percentages are being used in innovative ways.
E-commerce and Retail
In e-commerce, percentages are used extensively to optimize pricing strategies and marketing campaigns. A/B testing, where different versions of a product page or advertisement are shown to different groups of users, relies heavily on percentage analysis to determine which version performs better. Conversion rates, which are expressed as percentages, measure the proportion of visitors who complete a desired action, such as making a purchase.
Furthermore, personalized marketing campaigns use percentages to segment customers based on their purchasing behavior. For example, retailers might target customers who have a 20% higher likelihood of buying a specific product based on their past purchases.
Finance and Investment
In finance, percentages are fundamental for calculating returns on investment (ROI), interest rates, and portfolio allocations. Modern portfolio theory uses percentages to determine the optimal mix of assets to minimize risk and maximize returns. Robo-advisors, which use algorithms to manage investments, rely on percentage-based models to adjust portfolio allocations based on market conditions and investor risk profiles.
Additionally, the rise of cryptocurrencies has introduced new percentage-based metrics, such as the percentage change in the value of a cryptocurrency over a specific period. These metrics help investors assess the volatility and potential returns of these digital assets.
Healthcare
Percentages play a crucial role in healthcare analytics and patient care. They are used to measure the effectiveness of treatments, track disease prevalence, and monitor patient outcomes. For example, the success rate of a particular surgery might be expressed as a percentage, providing patients and healthcare providers with a clear understanding of the procedure’s effectiveness.
Moreover, percentages are used in public health to track vaccination rates and assess the impact of public health interventions. The percentage of the population vaccinated against a particular disease is a key indicator of herd immunity and the potential for outbreaks.
Education
In education, percentages are used to assess student performance and track academic progress. Grades are often expressed as percentages, providing a standardized measure of achievement. Additionally, percentages are used to analyze educational trends and identify areas where students may need additional support.
The use of data analytics in education is also growing, with percentages being used to identify at-risk students and personalize learning experiences. For example, if a student’s performance in a particular subject falls below a certain percentage threshold, interventions can be implemented to help them improve.
Professional Insights
Staying updated with these trends requires professionals to have a strong understanding of how percentages are used and interpreted in their respective fields. Here are some professional insights:
- Data Literacy: Being able to critically evaluate data presented as percentages is crucial for making informed decisions. This includes understanding the context in which the percentages are used and recognizing potential biases or limitations.
- Statistical Analysis: Professionals should be proficient in using statistical tools to analyze percentage-based data and identify meaningful trends and patterns.
- Communication: Effectively communicating percentage-based findings to stakeholders is essential. This involves presenting data in a clear and concise manner and explaining the implications of the findings.
- Continuous Learning: The applications of percentages are constantly evolving, so professionals should stay updated with the latest trends and developments in their fields.
By keeping up with these trends and developing the necessary skills, professionals can leverage the power of percentages to drive innovation and improve outcomes in their respective industries.
Tips and Expert Advice for Mastering Percentage Calculations
Mastering percentage calculations involves more than just understanding the basic formulas. Here are some practical tips and expert advice to help you enhance your skills and apply percentages effectively in real-world scenarios.
1. Practice Regularly
The key to mastering any mathematical concept is practice. Regularly solving percentage problems will help you become more comfortable with the formulas and improve your speed and accuracy.
- Real-Life Scenarios: Try to incorporate percentage calculations into your daily life. For example, calculate the tip at a restaurant, determine the discount on a sale item, or track your savings as a percentage of your income.
- Online Resources: Utilize online resources such as websites and apps that offer practice problems and quizzes on percentage calculations. These resources often provide immediate feedback, helping you identify areas where you need improvement.
- Workbooks and Textbooks: Work through practice problems in math workbooks or textbooks. These resources typically offer a wide range of problems with varying levels of difficulty.
2. Understand the Context
Percentages are often used in different contexts, and it's important to understand the specific context to interpret them correctly.
- Financial Context: In finance, percentages are used to express interest rates, investment returns, and debt-to-income ratios. Understanding these percentages is crucial for making informed financial decisions.
- Statistical Context: In statistics, percentages are used to summarize and compare data sets. It's important to understand the sample size and potential biases when interpreting statistical percentages.
- Retail Context: In retail, percentages are used to express discounts and sales tax rates. Understanding these percentages helps you determine the actual cost of a product.
3. Use Mental Math Techniques
Developing mental math skills can help you quickly estimate percentages and make calculations on the fly.
- Breaking Down Percentages: Break down complex percentages into simpler ones. For example, to calculate 15% of a number, calculate 10% and 5% separately and then add them together.
- Using Benchmarks: Use benchmark percentages such as 10%, 25%, and 50% as reference points. For example, 25% is one-quarter, 50% is one-half, and 10% is one-tenth.
- Estimating: Round numbers to make mental calculations easier. For example, to calculate 18% of 203, round 203 to 200 and calculate 18% of 200.
4. Convert Percentages to Decimals and Fractions
Being able to convert percentages to decimals and fractions can simplify calculations and improve your understanding of percentages.
- Decimal Conversion: To convert a percentage to a decimal, divide it by 100. For example, 30% = 0.30.
- Fraction Conversion: To convert a percentage to a fraction, write it as a fraction with a denominator of 100 and then simplify. For example, 40% = 40/100 = 2/5.
5. Avoid Common Mistakes
Avoid common mistakes when working with percentages to ensure accuracy.
- Misunderstanding the Base: Always identify the base or whole number to which the percentage is applied. For example, a 10% increase followed by a 10% decrease does not result in the original number because the base changes.
- Confusing Percentage Points with Percentages: Understand the difference between percentage points and percentages. For example, if an interest rate increases from 5% to 7%, it has increased by 2 percentage points or by 40%.
- Forgetting to Convert: Remember to convert percentages to decimals or fractions before performing calculations.
6. Seek Expert Advice
Consult with experts or mentors to gain deeper insights and personalized advice on mastering percentage calculations.
- Teachers and Tutors: Seek help from math teachers or tutors who can provide additional guidance and support.
- Financial Advisors: Consult with financial advisors for advice on using percentages in financial planning and investment decisions.
- Online Communities: Participate in online forums and communities to learn from others and share your own knowledge and experiences.
By following these tips and expert advice, you can enhance your percentage calculation skills and apply them effectively in various real-world scenarios.
FAQ: Frequently Asked Questions About Percentages
To further clarify the concept of percentages, here are some frequently asked questions with concise and informative answers.
Q: What does "percent" mean?
A: "Percent" comes from the Latin per centum, meaning "per hundred." It is a way of expressing a number as a fraction of 100.
Q: How do you convert a percentage to a decimal?
A: To convert a percentage to a decimal, divide the percentage by 100. For example, 75% = 75 / 100 = 0.75.
Q: How do you convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100. For example, 0.45 = 0.45 × 100 = 45%.
Q: How do you calculate the percentage increase or decrease?
A: To calculate the percentage increase or decrease:
- Percentage Change = ((New Value - Old Value) / Old Value) × 100
- A positive result indicates an increase, while a negative result indicates a decrease.
Q: What is the difference between percentage and percentage points?
A: A percentage is a ratio expressed as a fraction of 100, while percentage points refer to the arithmetic difference between two percentages. For example, if an interest rate increases from 5% to 7%, it has increased by 2 percentage points or by 40%.
Q: How do you find what percentage one number is of another?
A: To find what percentage one number is of another, divide the part by the whole and then multiply by 100.
- Percentage = (Part / Whole) × 100
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This typically occurs when comparing a new value to an original value that has more than doubled. For example, if a company's revenue increases from $100 to $250, the percentage increase is 150%.
Q: How do you calculate a percentage of a percentage?
A: To calculate a percentage of a percentage, convert both percentages to decimals and then multiply them. For example, what is 20% of 50%?
-
- 20 × 0.50 = 0.10, which is 10%.
Q: Why is understanding percentages important?
A: Understanding percentages is crucial for financial literacy, data interpretation, everyday life, and problem-solving. They are used in various fields, including finance, statistics, retail, and education.
Conclusion
In summary, understanding five percent of 100 is a fundamental concept that serves as a building block for more complex percentage calculations. We’ve explored the basic definition of percentages, step-by-step methods for calculating them, real-world applications, and tips for mastering percentage calculations.
Being proficient with percentages is not just an academic exercise; it's a practical skill that enhances your ability to make informed decisions in various aspects of life, from finance to everyday shopping. By practicing regularly, understanding the context, and utilizing mental math techniques, you can become confident in your ability to work with percentages.
Now that you have a solid understanding of percentages, take the next step and apply your knowledge to real-world scenarios. Calculate discounts, estimate tips, and analyze data using percentages. The more you practice, the more confident and skilled you will become.
Call to Action: Share this article with friends or colleagues who could benefit from understanding percentages. Practice calculating different percentages daily to sharpen your skills. Leave a comment below sharing how you use percentages in your everyday life!
Latest Posts
Latest Posts
-
Where Did Louis Armstrong Grew Up
Nov 20, 2025
-
How To Solve Alternate Exterior Angles
Nov 20, 2025
-
What Does A Spring Balance Measure
Nov 20, 2025
-
What Mountain Range Is In Idaho
Nov 20, 2025
-
12 Oz Is How Many Lbs
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about What Is Five Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.