What Is 5 To The Power Of 0
sonusaeterna
Nov 15, 2025 · 11 min read
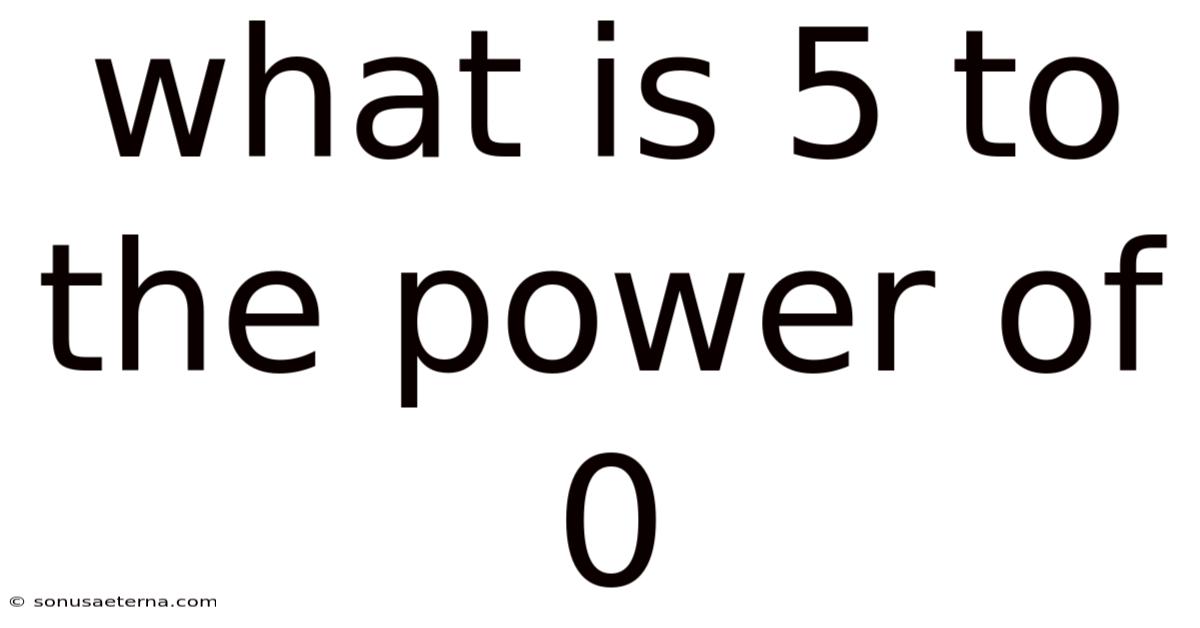
Table of Contents
Imagine you're at a bakery, and you want to buy some cupcakes. You ask for 5 cupcakes, then 5 squared (25) cupcakes for a party, and then 5 cubed (125) cupcakes because, well, who can resist? But then you change your mind and decide you don't need any cupcakes at all. How many cupcakes do you have? Zero, of course! But what if we express that as a power of 5? That's where the concept of 5 to the power of 0 comes in, and while it might seem counterintuitive, it’s not zero. Instead, it’s a fundamental concept in mathematics with a fascinating explanation.
Have you ever wondered why any number raised to the power of 0 equals 1? It's a question that often pops up in math class, leaving many scratching their heads. While it might seem like a bizarre mathematical rule, there's a logical and consistent explanation behind it. Understanding this concept is crucial for mastering algebra, calculus, and various other mathematical disciplines. This article will delve into the intricacies of 5 to the power of 0, exploring its definition, mathematical foundations, practical applications, and addressing some common misconceptions. By the end, you’ll have a solid grasp on why 5⁰ = 1 and appreciate the beauty and consistency of mathematical rules.
Main Subheading
To understand why 5 to the power of 0 equals 1, it’s essential to first grasp the basic principles of exponents. Exponents, also known as powers, are a way of expressing repeated multiplication. For example, 5 to the power of 3 (written as 5³) means 5 multiplied by itself three times: 5 x 5 x 5 = 125. The number 5 is called the base, and the number 3 is the exponent or power. Exponents provide a concise way to write and work with large numbers, making them indispensable in various fields such as science, engineering, and finance.
The concept of exponents extends beyond simple multiplication. They are governed by certain rules that allow us to simplify and manipulate expressions. One of the fundamental rules of exponents is the quotient rule, which states that when dividing two exponential expressions with the same base, you subtract the exponents. Mathematically, this is expressed as a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. This rule is crucial in understanding why any number raised to the power of 0 equals 1. By applying this rule, we can derive the value of 5⁰ and see how it fits perfectly within the framework of exponential rules.
Comprehensive Overview
Let's delve deeper into the mathematical foundations and explore how the concept of 5 to the power of 0 arises naturally from the rules of exponents. The explanation lies in maintaining consistency within the mathematical framework. Consider the quotient rule of exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. Now, let's say we have a<sup>m</sup> / a<sup>m</sup>. According to the rule, this simplifies to a<sup>m-m</sup> = a<sup>0</sup>. However, any number divided by itself is equal to 1. Therefore, a<sup>m</sup> / a<sup>m</sup> = 1. Combining these two results, we get a<sup>0</sup> = 1.
Applying this to our specific case, 5 to the power of 0 (5⁰) can be thought of as 5<sup>n</sup> / 5<sup>n</sup> for any number n. For instance, let's take n = 3. So, we have 5³ / 5³. This is equal to (5 x 5 x 5) / (5 x 5 x 5) = 125 / 125 = 1. According to the quotient rule, 5³ / 5³ = 5<sup>3-3</sup> = 5⁰. Therefore, 5⁰ must equal 1 to maintain the consistency of the exponent rules.
Another way to understand this concept is by observing the pattern of decreasing exponents. Let's look at the powers of 5:
- 5⁴ = 625
- 5³ = 125
- 5² = 25
- 5¹ = 5
Notice that as the exponent decreases by 1, the result is divided by 5. Following this pattern, if we decrease the exponent by 1 again, we get:
- 5⁰ = 5¹ / 5 = 5 / 5 = 1
This pattern consistently shows that 5 to the power of 0 must equal 1 to maintain the mathematical harmony and continuity of exponential functions. If 5⁰ were equal to any other number, it would disrupt the established rules and patterns of exponents.
Historically, the concept of zero as an exponent developed gradually as mathematicians sought to create a cohesive and consistent system. Early mathematicians like Brahmagupta in India (around 628 AD) recognized the importance of zero in mathematical operations, but the formalization of zero as an exponent came later. The development of exponential notation and the rules governing exponents were crucial steps in this process. As mathematicians refined these rules, they realized that defining any number to the power of zero as 1 was the only way to maintain consistency and coherence.
The definition of 5⁰ = 1 is not just an arbitrary rule; it's a logical necessity that arises from the fundamental principles of exponents and mathematical consistency. This definition allows for seamless integration of exponential functions into various mathematical operations and ensures that the rules of exponents hold true across all scenarios.
Trends and Latest Developments
In contemporary mathematics, the principle of 5⁰ = 1 remains a cornerstone in various advanced fields. While the basic concept is well-established, its application and implications continue to be relevant in modern mathematical research and practical applications. For instance, in areas like calculus and differential equations, understanding this rule is essential for simplifying expressions and solving complex problems.
One area where this principle is particularly relevant is in the study of power series. A power series is an infinite series of the form Σ a<sub>n</sub>(x - c)<sup>n</sup>, where a<sub>n</sub> represents the coefficients, x is a variable, and c is a constant. When n = 0, the term becomes a<sub>0</sub>(x - c)⁰. According to the rule, (x - c)⁰ = 1, so the term simplifies to a<sub>0</sub>. This simplification is crucial for evaluating the power series and understanding its convergence properties. Without the definition of 5⁰ = 1 (or any number to the power of 0 equals 1), the entire framework of power series would be inconsistent.
Moreover, in computer science, particularly in algorithms and data analysis, the principle of 5⁰ = 1 is implicitly used in various computational processes. For example, when dealing with polynomial functions or exponential growth models, understanding the behavior of functions as they approach zero is essential. In these contexts, the consistent application of the rule helps in accurately modeling and predicting real-world phenomena.
Recent trends in mathematical education emphasize a deeper understanding of fundamental concepts rather than rote memorization. Educators are increasingly using interactive tools and visual aids to demonstrate why 5⁰ = 1, helping students grasp the underlying logic and appreciate the beauty of mathematical consistency. This approach fosters a more intuitive understanding of mathematics, making it accessible and engaging for students of all levels.
Professional insights from mathematicians and educators highlight the importance of this rule in building a solid foundation in mathematics. They argue that a thorough understanding of basic principles like 5⁰ = 1 is crucial for tackling more advanced topics and for developing critical thinking skills. This emphasis on conceptual understanding reflects a broader trend in education towards fostering deeper, more meaningful learning experiences.
Tips and Expert Advice
To truly master the concept of 5 to the power of 0, it's essential not just to memorize the rule, but to understand its implications and applications. Here are some practical tips and expert advice to help you solidify your understanding:
First, practice applying the quotient rule of exponents. This rule is the key to understanding why any number to the power of 0 equals 1. Take different examples of exponential expressions and simplify them using the quotient rule. For instance, try simplifying (7<sup>5</sup> / 7<sup>5</sup>), (3<sup>2</sup> / 3<sup>2</sup>), and (10<sup>4</sup> / 10<sup>4</sup>). Each of these will simplify to 1, demonstrating that the base raised to the power of 0 is always 1. This hands-on practice will reinforce the logical connection between the rule and the result.
Second, visualize the pattern of decreasing exponents. Creating a table of exponents for a specific base can help you see how the values change as the exponent decreases. Start with a higher exponent (e.g., 5⁴) and decrease it by 1 each time, calculating the corresponding value. Notice how each value is divided by the base as the exponent decreases. This visual representation will make it clear that 5⁰ must equal 1 to maintain the pattern. For example:
- 5⁴ = 625
- 5³ = 125
- 5² = 25
- 5¹ = 5
- 5⁰ = 1
Third, explore real-world applications of exponents. Understanding how exponents are used in various fields can make the concept more relevant and engaging. Look into examples of exponential growth and decay in biology, finance, and physics. Seeing how exponential functions are used to model real-world phenomena will help you appreciate the importance of understanding the rules of exponents, including the rule for 5 to the power of 0.
Fourth, address common misconceptions. Many students mistakenly believe that 5⁰ equals 0 or that it is undefined. It's important to understand why these beliefs are incorrect. Emphasize that defining 5⁰ as 1 is necessary to maintain consistency with the rules of exponents. If 5⁰ were equal to 0 or undefined, it would create contradictions and inconsistencies in mathematical operations.
Fifth, use interactive tools and online resources. There are many online calculators, tutorials, and interactive tools that can help you visualize and explore the concept of exponents. Websites like Khan Academy, Wolfram Alpha, and Desmos offer valuable resources for learning and practicing exponent rules. These tools can provide a dynamic and engaging way to deepen your understanding.
Finally, teach the concept to someone else. One of the best ways to solidify your understanding of a concept is to explain it to someone else. Try explaining why 5⁰ = 1 to a friend or family member. This will force you to organize your thoughts and articulate the reasoning behind the rule. If you can successfully explain the concept to someone else, you'll know that you truly understand it.
FAQ
Q: Why does any number to the power of 0 equal 1? A: Any number to the power of 0 equals 1 to maintain consistency with the rules of exponents, particularly the quotient rule (a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>). When m = n, a<sup>m</sup> / a<sup>m</sup> = 1, and a<sup>m-m</sup> = a<sup>0</sup>. Therefore, a<sup>0</sup> = 1.
Q: Does 0 to the power of 0 also equal 1? A: The expression 0⁰ is generally considered to be undefined in many contexts. While in some specific cases, it might be defined as 1 for convenience (e.g., in combinatorics or power series), it is not universally agreed upon, and its value depends on the context.
Q: What if I still find it hard to believe that 5⁰ = 1? A: It's common to find this concept counterintuitive. Try revisiting the pattern of decreasing exponents or working through examples using the quotient rule. The key is to understand the logical necessity for this rule to maintain mathematical consistency.
Q: Are there any exceptions to the rule that any number to the power of 0 equals 1? A: The main exception is 0⁰, which is often undefined. For all other non-zero numbers, the rule holds true.
Q: How is this concept used in real-world applications? A: The concept is used in various fields, including calculus, computer science, and finance. It is particularly important in power series, polynomial functions, and exponential growth models, where consistent application of the rule is crucial for accurate calculations and predictions.
Conclusion
Understanding that 5 to the power of 0 equals 1 is more than just memorizing a mathematical rule; it's about appreciating the underlying logic and consistency that governs the world of mathematics. By exploring the quotient rule of exponents, observing patterns of decreasing exponents, and addressing common misconceptions, we can see how this definition arises naturally from the foundational principles of exponents. This understanding is not only crucial for academic success but also for developing a deeper appreciation of the elegance and coherence of mathematical systems.
Now that you have a solid grasp of why 5⁰ = 1, why not put your knowledge to the test? Try solving some practice problems involving exponents and share your insights with others. Engage in discussions about the applications of exponents in real-world scenarios and continue to explore the fascinating world of mathematics. Don't hesitate to delve deeper into related topics like power series, exponential functions, and logarithmic scales to further enrich your understanding. The journey of mathematical discovery is endless, and every step brings new insights and perspectives.
Latest Posts
Latest Posts
-
Which President Cut Down A Cherry Tree
Nov 15, 2025
-
Michael Mann Sources Of Social Power
Nov 15, 2025
-
What Are The Physical Properties Of Metals
Nov 15, 2025
-
How To Study For Ap Gov Test
Nov 15, 2025
-
Whats The Difference Between A Reptile And An Amphibian
Nov 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 To The Power Of 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.