What Is 3/8 Plus 1/2 In Fraction Form
sonusaeterna
Nov 27, 2025 · 11 min read
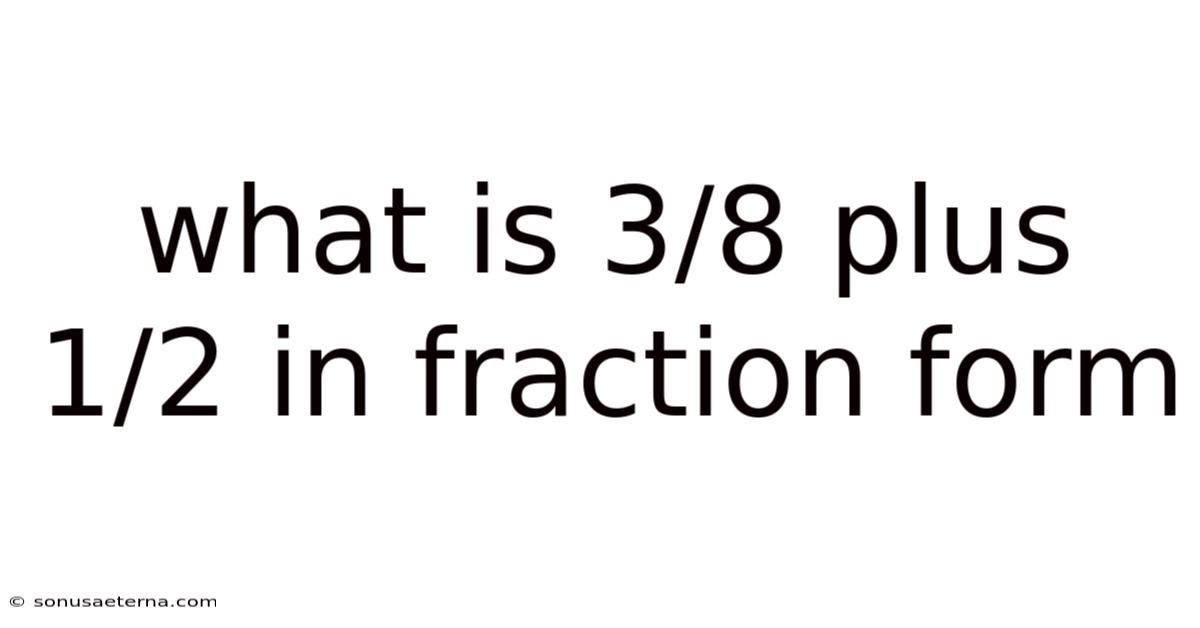
Table of Contents
Imagine you're baking a cake for a friend's birthday. The recipe calls for 3/8 of a cup of flour and 1/2 a cup of sugar. You grab your measuring cups, but then you wonder, "How much do I have in total? Can I just use one big measuring cup instead of two?" To figure that out, you need to know how to add these fractions together. It's not just about baking; understanding how to add fractions like 3/8 and 1/2 is useful in many everyday situations, from splitting a pizza to managing your finances.
Fractions are more than just numbers on a page; they're a fundamental part of how we understand proportions and parts of a whole. Knowing how to perform arithmetic operations with fractions, such as adding 3/8 and 1/2, is a critical skill. This article will walk you through the process step by step, ensuring that by the end, you'll not only be able to solve this particular problem but also understand the underlying principles so you can tackle any fraction addition with confidence. Let's dive in and make fractions a piece of cake!
Main Subheading
Adding fractions might seem daunting at first, but it becomes straightforward once you grasp the underlying principles. At its core, adding fractions requires a common denominator. This is because you can only directly add or subtract fractions when they represent parts of the same-sized whole. Think of it like trying to add apples and oranges; you need a common unit, like "fruits," to combine them meaningfully. Similarly, fractions need a common denominator to be combined.
The concept of a common denominator ensures that we are dealing with comparable "slices" of the same "pie." When fractions have the same denominator, we can simply add their numerators (the top numbers) to find the total number of those slices. If the denominators are different, we must first convert the fractions into equivalent forms with a common denominator before adding. This involves finding a multiple that both denominators share and adjusting the numerators accordingly to maintain the fractions' values. Once this is done, the addition becomes as simple as adding whole numbers.
Comprehensive Overview
Defining Fractions
A fraction is a way to represent a part of a whole. It consists of two numbers: the numerator and the denominator. The numerator (the top number) indicates how many parts we have, while the denominator (the bottom number) indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/8, "3" is the numerator, and "8" is the denominator. This means we have 3 parts out of a total of 8 equal parts.
The Need for a Common Denominator
To add or subtract fractions, they must have a common denominator. This is because you can only directly add or subtract quantities that are measured in the same units. When fractions have the same denominator, they are said to be "like fractions." Adding like fractions is simple: you just add the numerators and keep the denominator the same.
For instance, if you want to add 2/5 and 1/5, both fractions have the same denominator (5). Therefore, you add the numerators (2 + 1) and keep the denominator the same, resulting in 3/5. This is straightforward and intuitive.
However, when fractions have different denominators, they are called "unlike fractions." In this case, you can't directly add the numerators. You need to find a common denominator first. This common denominator is a multiple that both denominators share. Once you have a common denominator, you convert each fraction into an equivalent fraction with that denominator.
Finding the Least Common Denominator (LCD)
The Least Common Denominator (LCD) is the smallest common multiple of the denominators of two or more fractions. Finding the LCD simplifies the addition process and ensures that the resulting fraction is in its simplest form more easily. There are several methods to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find a common multiple. For example, to find the LCD of 8 and 2, list the multiples of 8 (8, 16, 24, ...) and the multiples of 2 (2, 4, 6, 8, 10, ...). The smallest multiple they have in common is 8, so the LCD is 8.
-
Prime Factorization: Break down each denominator into its prime factors. Then, take the highest power of each prime factor that appears in any of the denominators and multiply them together. For example, to find the LCD of 8 and 2:
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 2: 2
- The highest power of 2 that appears is 2³, so the LCD is 2³ = 8.
Converting to Equivalent Fractions
Once you've found the LCD, you need to convert each fraction into an equivalent fraction with the LCD as its denominator. To do this, divide the LCD by the original denominator and then multiply both the numerator and the denominator of the original fraction by the result. This ensures that the value of the fraction remains unchanged while the denominator is adjusted to the LCD.
For example, to convert 1/2 to an equivalent fraction with a denominator of 8, divide 8 (the LCD) by 2 (the original denominator), which gives you 4. Then, multiply both the numerator and the denominator of 1/2 by 4:
- (1 x 4) / (2 x 4) = 4/8
Now, 1/2 is equivalent to 4/8, and both fractions have the same denominator, making it possible to add them.
Adding the Fractions
Once the fractions have a common denominator, you can add them by simply adding the numerators and keeping the denominator the same. This results in a new fraction that represents the sum of the original fractions.
For example, after converting 1/2 to 4/8, you can add 3/8 and 4/8:
- 3/8 + 4/8 = (3 + 4) / 8 = 7/8
So, the sum of 3/8 and 1/2 is 7/8.
Trends and Latest Developments
In mathematics education, there is an increasing emphasis on conceptual understanding rather than rote memorization. This trend encourages educators to focus on why fractions are added the way they are, rather than just how to do it. Visual aids, such as fraction bars and pie charts, are commonly used to help students grasp the concept of common denominators and equivalent fractions. These tools provide a concrete way to see how fractions relate to each other and how they can be combined.
Digital tools and educational software also play a significant role in teaching fractions. Interactive simulations and games can make learning fractions more engaging and help students practice adding fractions in a fun and dynamic way. These resources often provide immediate feedback, allowing students to correct their mistakes and reinforce their understanding.
Recent research in math education highlights the importance of addressing common misconceptions about fractions early on. For example, many students mistakenly believe that they can simply add the numerators and denominators of fractions without finding a common denominator. Educators are now focusing on strategies to identify and correct these misconceptions through targeted instruction and practice.
Additionally, there is a growing trend towards integrating mathematical concepts with real-world applications. This approach helps students see the relevance of fractions in everyday life and motivates them to learn. Examples include using fractions in cooking, measuring, and financial literacy.
Tips and Expert Advice
Adding fractions can become second nature with the right approach and consistent practice. Here are some expert tips to help you master this essential skill:
- Always Simplify First: Before you even start looking for a common denominator, check if either of the fractions can be simplified. Simplifying fractions early can make the numbers smaller and easier to work with, reducing the complexity of the problem. To simplify a fraction, divide both the numerator and the denominator by their greatest common factor (GCF). For example, if you were adding 4/8 to another fraction, simplify 4/8 to 1/2 first.
- Master the Multiplication Table: A strong grasp of multiplication tables is invaluable when working with fractions. Knowing your multiples makes it much easier to identify common denominators and convert fractions to equivalent forms. Dedicate some time to memorizing or regularly reviewing your multiplication tables; it will pay off in the long run.
- Use Visual Aids: Visual aids can be incredibly helpful for understanding fractions, especially when you're first learning. Draw diagrams or use physical manipulatives like fraction bars or pie charts to visualize the fractions and their relationships. Seeing the fractions visually can make the abstract concepts more concrete and easier to grasp.
- Estimate Your Answer: Before performing the addition, take a moment to estimate what the answer should be. This can help you catch mistakes and ensure that your final answer is reasonable. For example, if you're adding 3/8 and 1/2, you know that 3/8 is a little less than 1/2, so the answer should be a little less than 1.
- Practice Regularly: Like any math skill, mastering fractions requires regular practice. Set aside some time each day or week to work on fraction problems. Start with simple problems and gradually work your way up to more complex ones. The more you practice, the more confident and proficient you'll become.
- Understand the "Why": Don't just memorize the steps for adding fractions; make sure you understand why those steps are necessary. Knowing the underlying principles will help you apply the concepts to different types of problems and remember the process more effectively. For example, understand why fractions need a common denominator before they can be added, rather than just memorizing that you need to find one.
- Check Your Work: After you've added the fractions, take a moment to check your work. Make sure you've found the correct common denominator, converted the fractions correctly, and added the numerators accurately. If possible, use a calculator or online tool to verify your answer.
FAQ
Q: Why do fractions need a common denominator before adding?
A: Fractions need a common denominator because you can only add or subtract quantities that are measured in the same units. A common denominator ensures that you are adding "slices" of the same size, making the addition meaningful.
Q: What is the Least Common Denominator (LCD)?
A: The Least Common Denominator (LCD) is the smallest common multiple of the denominators of two or more fractions. It simplifies the addition process and helps ensure the resulting fraction is in its simplest form.
Q: How do I find the LCD?
A: You can find the LCD by listing the multiples of each denominator until you find a common multiple, or by using prime factorization to break down each denominator into its prime factors and then taking the highest power of each prime factor.
Q: What is an equivalent fraction?
A: An equivalent fraction is a fraction that has the same value as another fraction but with a different numerator and denominator. For example, 1/2 and 2/4 are equivalent fractions.
Q: How do I convert a fraction to an equivalent fraction with a different denominator?
A: To convert a fraction to an equivalent fraction with a different denominator, divide the new denominator by the original denominator, and then multiply both the numerator and the denominator of the original fraction by the result.
Conclusion
Adding fractions is a fundamental skill that has applications far beyond the classroom. From cooking and baking to managing finances and understanding proportions, knowing how to work with fractions is essential in everyday life. This article has provided a comprehensive guide to adding fractions, focusing on the specific example of adding 3/8 and 1/2. By understanding the need for a common denominator, finding the Least Common Denominator (LCD), and converting fractions to equivalent forms, you can confidently add any fractions together.
Remember, the key to mastering fractions is consistent practice and a solid understanding of the underlying principles. Use visual aids, estimate your answers, and always check your work to ensure accuracy. With these tips and techniques, you'll be well on your way to becoming a fraction expert. Now that you have a solid grasp of adding fractions, put your knowledge to the test! Try solving more fraction problems and explore how fractions are used in real-world scenarios. Share your newfound expertise with friends and family, and help them conquer their fear of fractions too. Do you have any tips or tricks for adding fractions? Share them in the comments below and let's continue the learning journey together!
Latest Posts
Latest Posts
-
How Do You Construct An Altitude Of A Triangle
Nov 27, 2025
-
What Is Local Maximum On A Graph
Nov 27, 2025
-
How Long Is The Chesapeake Bay Tunnel
Nov 27, 2025
-
How Fast Can The Fastest Bird Fly
Nov 27, 2025
-
Longest Mountain Range In North America
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/8 Plus 1/2 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.