What Is 3/4 As A Fraction
sonusaeterna
Nov 22, 2025 · 11 min read
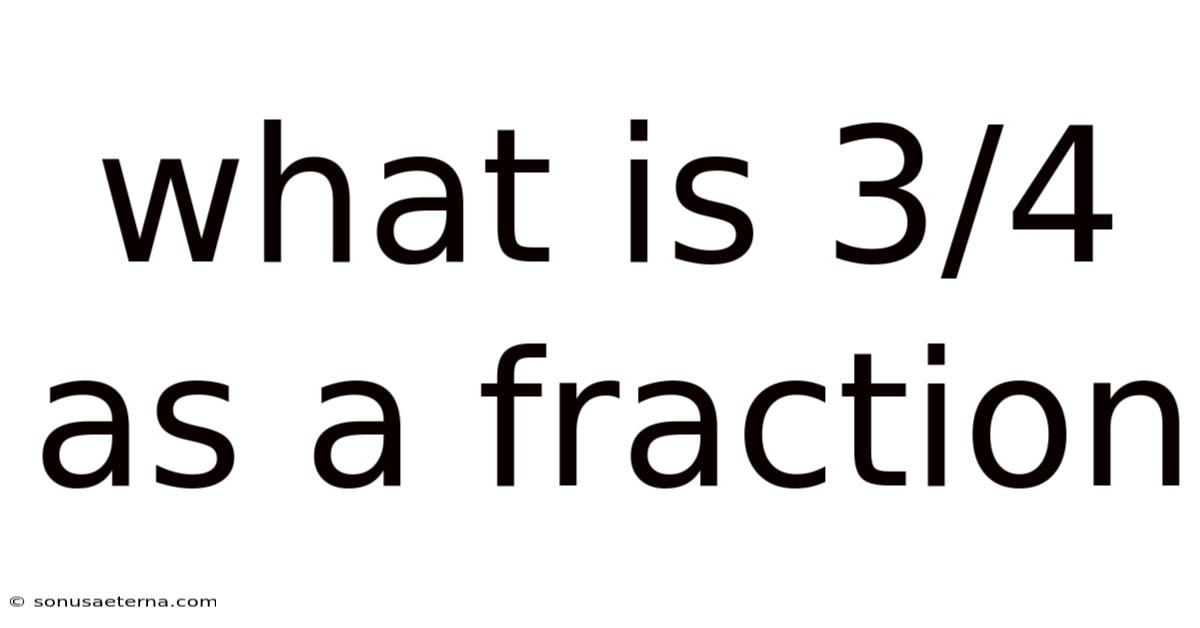
Table of Contents
Imagine slicing a pizza into four equal pieces. You grab three of those slices, leaving just one behind. That’s essentially what the fraction 3/4 represents – three parts out of a total of four. Fractions, at their core, are about understanding parts of a whole. They're a fundamental concept in mathematics and a crucial stepping stone to more advanced topics.
Think about baking a cake. A recipe might call for 3/4 cup of flour. This means you need a quantity of flour that's less than a full cup, but more than half. Understanding how to work with fractions like 3/4 allows you to accurately measure ingredients, divide resources fairly, and make sense of proportions in various aspects of life. This article will provide a comprehensive understanding of what the fraction 3/4 means, how it relates to other fractions and decimals, and its practical applications.
Understanding the Fraction 3/4
The fraction 3/4 is a common sight in everyday life, from cooking recipes to dividing tasks among a group. To truly grasp its meaning, it’s important to understand its basic structure and how it fits into the broader world of fractions.
At its heart, a fraction represents a part of a whole. This "whole" can be anything – a pizza, a cake, a length of rope, or even a set of objects. The fraction itself is written as two numbers separated by a horizontal line. The number above the line is called the numerator, and the number below the line is called the denominator. In the case of 3/4, the numerator is 3 and the denominator is 4.
The denominator tells us how many equal parts the whole has been divided into. So, in the fraction 3/4, the whole has been divided into 4 equal parts. The numerator tells us how many of these parts we are considering. Therefore, 3/4 represents 3 of those 4 equal parts. It's crucial that these parts are equal for the fraction to be accurate. If you're dividing a pizza, each slice must be the same size for the fraction to be a true representation. If one slice is significantly larger than the others, the fraction 3/4 would no longer accurately describe the portion you have.
Comprehensive Overview of Fractions
To fully understand the fraction 3/4, it's helpful to have a broader understanding of fractions in general. Fractions have been used for thousands of years, with evidence of their use dating back to ancient civilizations like the Egyptians and Babylonians. These early uses were primarily for practical purposes, such as dividing land, measuring quantities, and calculating taxes.
Fractions can be categorized in several ways. One way is to distinguish between proper fractions and improper fractions. A proper fraction is one where the numerator is less than the denominator, like 3/4. This means it represents a value less than one whole. An improper fraction, on the other hand, has a numerator that is greater than or equal to the denominator, such as 5/4. This represents a value greater than or equal to one whole. Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction (e.g., 5/4 is equivalent to 1 1/4).
Fractions can also be equivalent. Equivalent fractions represent the same value even though they have different numerators and denominators. For example, 3/4 is equivalent to 6/8, 9/12, and 12/16. To find equivalent fractions, you can multiply or divide both the numerator and denominator by the same non-zero number. This process maintains the proportion and ensures the value remains the same. Understanding equivalent fractions is crucial for simplifying fractions and performing arithmetic operations with them.
Another important concept is the simplest form of a fraction. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1. To simplify a fraction, you divide both the numerator and denominator by their greatest common factor (GCF). For example, the GCF of 6 and 8 is 2. So, simplifying 6/8 involves dividing both 6 and 8 by 2, resulting in 3/4, which is the simplest form. Simplifying fractions makes them easier to understand and work with.
Fractions are closely related to decimals and percentages. A fraction can be converted into a decimal by dividing the numerator by the denominator. For example, 3/4 is equal to 0.75. A decimal can be converted into a percentage by multiplying it by 100. So, 0.75 is equal to 75%. These conversions are useful for comparing and interpreting different representations of the same value. Understanding the relationship between fractions, decimals, and percentages is essential for various applications, including finance, statistics, and everyday calculations.
Trends and Latest Developments
While the basic concept of fractions remains unchanged, their application and understanding continue to evolve. Recent trends in mathematics education emphasize a deeper, more conceptual understanding of fractions rather than rote memorization of rules. This involves using visual aids, hands-on activities, and real-world examples to help students grasp the meaning of fractions and their operations.
Data from educational research highlights the importance of early intervention for students struggling with fractions. Difficulties with fractions in elementary school can have a cascading effect, hindering progress in more advanced math courses. Therefore, educators are focusing on identifying and addressing these difficulties early on, using targeted interventions and personalized learning strategies.
Another trend is the increasing use of technology in teaching fractions. Interactive simulations, online games, and educational apps provide students with engaging ways to explore fractions and practice their skills. These tools can help visualize abstract concepts, provide immediate feedback, and adapt to individual learning needs. However, it's important to use technology as a supplement to, rather than a replacement for, traditional teaching methods. A balanced approach that combines hands-on activities, conceptual understanding, and technology can be most effective.
In the professional world, a solid understanding of fractions remains crucial in various fields, including engineering, finance, and construction. Engineers use fractions to calculate proportions and tolerances, while financial analysts use them to analyze investments and assess risk. In construction, fractions are essential for measuring materials and ensuring accuracy in building projects. The ability to work confidently with fractions is a valuable asset in these and many other professions.
Furthermore, there's a growing recognition of the importance of numerical literacy in everyday life. This includes the ability to understand and interpret fractions, decimals, and percentages in various contexts, such as reading news articles, managing personal finances, and making informed decisions about health and nutrition. Improving numerical literacy is essential for empowering individuals to navigate the complexities of modern life and make sound judgments.
Tips and Expert Advice
Understanding and working with fractions, especially 3/4, can be made easier with a few practical tips and expert advice. These strategies can help you build a stronger foundation and apply your knowledge effectively.
Visualize Fractions: One of the most effective ways to understand fractions is to visualize them. Use diagrams, pictures, or real-world objects to represent the whole and its parts. For example, draw a circle and divide it into four equal parts. Shade three of those parts to represent 3/4. This visual representation can help you grasp the concept more intuitively. You can also use physical objects, such as blocks or measuring cups, to demonstrate fractions. For instance, fill a measuring cup to the 3/4 mark to visualize the quantity.
Practice Regularly: Like any skill, working with fractions requires practice. Solve a variety of problems involving fractions to reinforce your understanding and build confidence. Start with simple exercises and gradually move on to more complex ones. Use online resources, textbooks, or worksheets to find practice problems. The more you practice, the more comfortable you will become with fractions and their operations.
Relate to Real-World Examples: Connect fractions to real-world situations to make them more meaningful. Think about how fractions are used in cooking, shopping, and other everyday activities. For example, when following a recipe, you might need to double or halve the ingredients, which involves working with fractions. When shopping, you might see discounts expressed as percentages, which are closely related to fractions. By relating fractions to real-world examples, you can see their relevance and practical value.
Use Benchmarks: Use benchmark fractions, such as 1/2, 1/4, and 3/4, as reference points when comparing and estimating fractions. This can help you develop a better sense of the relative size of fractions. For example, if you need to estimate the sum of 3/4 and 1/3, you can think of 3/4 as being close to 1 and 1/3 as being close to 1/4. This can help you make a rough estimate of the sum without having to perform exact calculations.
Understand Equivalent Fractions: Mastering equivalent fractions is essential for simplifying fractions and performing arithmetic operations. Learn how to find equivalent fractions by multiplying or dividing both the numerator and denominator by the same number. This will allow you to express fractions in different forms while maintaining their value. For example, if you need to add 1/2 and 1/4, you can convert 1/2 to 2/4, which makes the addition easier.
Break Down Complex Problems: When faced with a complex problem involving fractions, break it down into smaller, more manageable steps. This can make the problem less daunting and easier to solve. For example, if you need to multiply 3/4 by a mixed number, convert the mixed number to an improper fraction first. Then, multiply the numerators and denominators separately. Finally, simplify the resulting fraction.
Seek Help When Needed: Don't hesitate to ask for help if you're struggling with fractions. Talk to your teacher, a tutor, or a friend who understands fractions well. There are also many online resources and tutorials that can provide additional explanations and examples. Remember that everyone learns at their own pace, and it's okay to ask for help when you need it.
FAQ
Q: What is the decimal equivalent of 3/4?
A: The decimal equivalent of 3/4 is 0.75. You can find this by dividing the numerator (3) by the denominator (4).
Q: Is 3/4 a proper or improper fraction?
A: 3/4 is a proper fraction because the numerator (3) is less than the denominator (4).
Q: How do you simplify the fraction 3/4?
A: The fraction 3/4 is already in its simplest form because the numerator (3) and denominator (4) have no common factors other than 1.
Q: Can 3/4 be expressed as a percentage?
A: Yes, 3/4 can be expressed as a percentage. To convert it to a percentage, multiply it by 100: (3/4) * 100 = 75%. So, 3/4 is equal to 75%.
Q: What are some real-world examples of using 3/4?
A: 3/4 is used in various real-world situations, such as: * Measuring ingredients in cooking (e.g., 3/4 cup of flour) * Expressing discounts (e.g., 3/4 off the original price) * Dividing tasks among a group (e.g., each person is responsible for 3/4 of the project) * Reading measurements on a ruler or measuring tape
Q: How do you add or subtract fractions with different denominators, such as 3/4 and 1/3?
A: To add or subtract fractions with different denominators, you need to find a common denominator first. The common denominator is the least common multiple (LCM) of the denominators. In this case, the LCM of 4 and 3 is 12. So, you need to convert both fractions to equivalent fractions with a denominator of 12. 3/4 becomes 9/12 (by multiplying both the numerator and denominator by 3), and 1/3 becomes 4/12 (by multiplying both the numerator and denominator by 4). Then, you can add or subtract the numerators while keeping the common denominator: * Adding: 9/12 + 4/12 = 13/12 * Subtracting: 9/12 - 4/12 = 5/12
Conclusion
The fraction 3/4 is more than just a mathematical symbol; it's a representation of a portion, a part of a whole that we encounter in countless scenarios. Understanding its meaning, its relationship to other fractions, decimals, and percentages, and its practical applications can greatly enhance your mathematical skills and your ability to navigate the world around you.
By mastering the concepts and tips discussed in this article, you can confidently work with fractions and apply them to solve real-world problems. Whether you're cooking in the kitchen, managing your finances, or pursuing a career in a STEM field, a solid understanding of fractions will serve you well. Take the next step and practice using 3/4 in different scenarios. Try adjusting a recipe, calculating a discount, or dividing a task among friends. The more you practice, the more comfortable and confident you will become with fractions. Share this article with friends or classmates who might benefit from understanding the meaning of 3/4, and continue exploring the fascinating world of mathematics!
Latest Posts
Latest Posts
-
What Account Type Is Common Stock
Nov 22, 2025
-
How To Find Adjective In A Sentence
Nov 22, 2025
-
Which Dwarves Died In The Hobbit
Nov 22, 2025
-
Examples Of Dominant And Recessive Traits
Nov 22, 2025
-
What Is Al On Periodic Table
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.