What Is 0.875 As A Fraction
sonusaeterna
Nov 28, 2025 · 10 min read
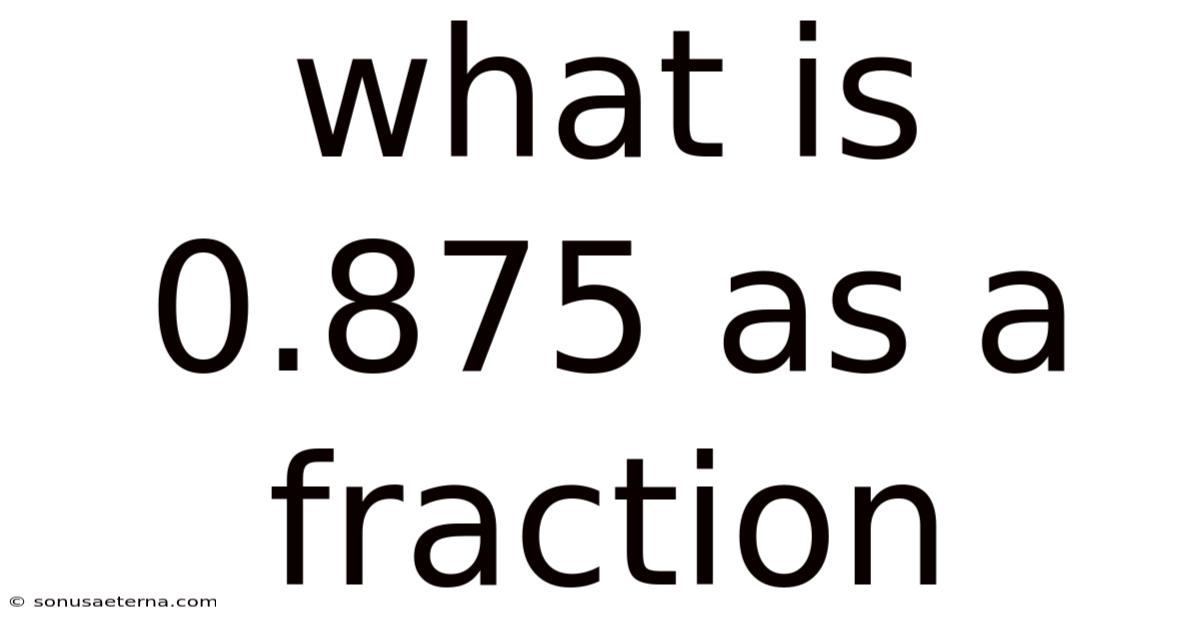
Table of Contents
The aroma of freshly baked bread filled the kitchen, a testament to my grandmother's precision. She measured ingredients with an almost scientific accuracy, muttering fractions and decimals under her breath. One day, while I was struggling with my math homework, she looked over my shoulder and saw the problem: converting 0.875 into a fraction. With a knowing smile, she set aside her dough and explained the simple elegance of transforming decimals into fractions. That moment demystified the process for me, turning a confusing problem into an understandable concept.
Like my grandmother transforming raw ingredients into a perfect loaf, converting decimals to fractions is about understanding the underlying structure. Decimals are simply another way of representing fractions with denominators that are powers of 10. The decimal 0.875, often encountered in measurements, recipes, and calculations, can seem daunting at first glance. But understanding its fractional equivalent unlocks a deeper comprehension of its value and simplifies many mathematical operations. This article will explore how to easily convert 0.875 into a fraction, providing a comprehensive overview, practical tips, and expert advice.
Main Subheading
Converting decimals into fractions is a fundamental skill in mathematics, bridging the gap between two different representations of the same numerical value. It's more than just a mechanical process; it's about understanding place value and the relationship between decimals and fractions. The ability to convert 0.875 into a fraction, for instance, allows for easier manipulation in certain calculations and a better grasp of its magnitude in real-world contexts.
This conversion process relies on recognizing that decimals are based on powers of 10. Each digit after the decimal point represents a fraction with a denominator that is a power of 10: tenths, hundredths, thousandths, and so on. Therefore, converting a decimal to a fraction involves expressing the decimal as a fraction with a power of 10 as the denominator, and then simplifying the fraction to its lowest terms. Mastering this skill not only enhances mathematical proficiency but also improves problem-solving abilities in various practical situations.
Comprehensive Overview
The journey of converting 0.875 into a fraction begins with understanding its underlying decimal structure. The decimal 0.875 represents eight tenths, seven hundredths, and five thousandths. This understanding forms the basis for the conversion process. Mathematically, we can express this as:
- 875 = (8/10) + (7/100) + (5/1000)
To convert 0.875 into a fraction, we express it as a fraction with a denominator that is a power of 10. Since 0.875 has three digits after the decimal point, we use 1000 as the denominator:
- 875 = 875/1000
This fraction is not yet in its simplest form. To simplify it, we need to find the greatest common divisor (GCD) of the numerator (875) and the denominator (1000) and divide both by it. The GCD of 875 and 1000 is 125. Dividing both the numerator and the denominator by 125, we get:
875 ÷ 125 = 7 1000 ÷ 125 = 8
Therefore, the simplified fraction is:
7/8
Thus, 0.875 as a fraction is 7/8. This means that 0.875 is equivalent to seven-eighths. Understanding this conversion allows us to see that 0.875 represents a quantity that is slightly less than one whole, specifically one-eighth less than a whole.
The scientific foundation for this conversion lies in the base-10 number system. Decimals are a natural extension of whole numbers, allowing us to represent quantities that are not whole numbers. Each position to the right of the decimal point represents a successively smaller power of 10. This system enables precise representation and manipulation of numbers, making calculations more accurate and efficient.
Historically, the development of decimal notation was a significant milestone in mathematics. Before decimals, fractions were the primary way to represent non-integer quantities. Decimals, however, provided a more intuitive and streamlined approach, particularly for calculations. The widespread adoption of decimals facilitated advancements in science, engineering, and commerce, allowing for more precise measurements and calculations.
The concept of place value is crucial in understanding decimal to fraction conversion. In the decimal 0.875, the '8' is in the tenths place, the '7' is in the hundredths place, and the '5' is in the thousandths place. This understanding allows us to decompose the decimal into its constituent parts, each of which can be easily expressed as a fraction.
Furthermore, understanding equivalent fractions is essential. The fraction 875/1000 is equivalent to 7/8 because both represent the same numerical value. Simplifying fractions involves finding the GCD of the numerator and denominator and dividing both by it. This process ensures that the fraction is expressed in its simplest form, making it easier to understand and work with.
In summary, converting 0.875 into a fraction involves understanding place value, powers of 10, and equivalent fractions. By expressing the decimal as a fraction with a power of 10 as the denominator and then simplifying the fraction, we can easily convert 0.875 into its fractional equivalent, which is 7/8.
Trends and Latest Developments
In today's digital age, calculators and software can instantly convert decimals to fractions. However, a solid understanding of the underlying mathematical principles remains crucial. While technology offers convenience, it is the conceptual understanding that allows for critical thinking and problem-solving in various contexts.
Recent trends in mathematics education emphasize conceptual understanding over rote memorization. Educators are increasingly focusing on teaching students the "why" behind mathematical procedures, rather than just the "how." This approach aims to foster a deeper appreciation for mathematics and improve students' ability to apply mathematical concepts in real-world situations.
Data from educational research indicates that students who have a strong conceptual understanding of fractions and decimals perform better in higher-level mathematics courses. This highlights the importance of mastering these fundamental concepts early on. Educators are using various pedagogical techniques, such as visual aids, manipulatives, and real-world examples, to help students develop a deeper understanding of fractions and decimals.
Popular opinion among mathematics educators is that students should be proficient in converting between decimals and fractions without relying solely on calculators. This proficiency enables students to estimate quantities, compare values, and perform mental calculations more effectively. It also enhances their overall number sense and mathematical intuition.
Professional insights suggest that the ability to convert decimals to fractions is particularly valuable in fields such as finance, engineering, and science. In finance, for example, understanding fractional representations of interest rates and investment returns is essential for making informed decisions. In engineering, precise measurements often involve both decimals and fractions, and the ability to convert between them is crucial for accuracy and efficiency. In science, converting decimals to fractions can simplify calculations and facilitate a better understanding of experimental results.
Moreover, the rise of data science and analytics has further underscored the importance of understanding decimals and fractions. Data is often presented in decimal form, and the ability to convert these decimals into fractions can provide valuable insights and facilitate data analysis. Professionals in these fields need to be able to work with both decimals and fractions fluently to extract meaningful information from data.
In conclusion, while technology offers convenient tools for converting decimals to fractions, a solid understanding of the underlying mathematical principles remains essential. Current trends in mathematics education emphasize conceptual understanding, and professionals in various fields benefit from the ability to work with decimals and fractions fluently.
Tips and Expert Advice
Converting decimals to fractions can be made easier with a few key tips and expert advice. First, always start by understanding the place value of the decimal. This will help you determine the correct power of 10 to use as the denominator. For example, in 0.875, the last digit '5' is in the thousandths place, so you know that the denominator will be 1000.
Next, remember to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. Simplifying the fraction makes it easier to understand and work with. For instance, 875/1000 can be simplified to 7/8 by dividing both by 125, their GCD.
Another helpful tip is to recognize common decimal-fraction equivalents. Knowing that 0.5 is equal to 1/2, 0.25 is equal to 1/4, and 0.125 is equal to 1/8 can save you time and effort when converting decimals to fractions. Recognizing these common equivalents allows for quick conversions without having to go through the full process each time.
Furthermore, practice converting decimals to fractions regularly. The more you practice, the more comfortable you will become with the process. Start with simple decimals and gradually work your way up to more complex ones. This practice will build your confidence and improve your speed and accuracy.
Expert advice includes using prime factorization to find the GCD. Prime factorization involves breaking down the numerator and denominator into their prime factors and then identifying the common factors. This method can be particularly helpful when dealing with larger numbers.
Another piece of expert advice is to use benchmarks. Benchmarks are common fractions and decimals that can be used as reference points. For example, if you are converting a decimal close to 0.5, you know that the fraction will be close to 1/2. Using benchmarks can help you estimate the fraction and check your work.
Additionally, consider using visual aids such as number lines and fraction bars to help you visualize the conversion process. These visual aids can make the abstract concepts of fractions and decimals more concrete and easier to understand.
Finally, remember that converting decimals to fractions is a skill that builds on other mathematical concepts. Make sure you have a solid understanding of place value, powers of 10, and equivalent fractions before attempting to convert decimals to fractions. This foundational knowledge will make the conversion process much easier and more intuitive.
By following these tips and expert advice, you can master the art of converting decimals to fractions and improve your overall mathematical proficiency. Remember to practice regularly, use visual aids, and focus on understanding the underlying concepts.
FAQ
Q: What is a decimal? A: A decimal is a way of representing numbers that are not whole numbers, using a base-10 system. It consists of a whole number part and a fractional part separated by a decimal point.
Q: What is a fraction? A: A fraction represents a part of a whole or, more generally, any number of equal parts. It is written as one number (the numerator) over another number (the denominator), indicating how many parts of a certain size are being represented.
Q: How do you convert a decimal to a fraction? A: To convert a decimal to a fraction, write the decimal as a fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000). Then, simplify the fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor.
Q: What is the greatest common divisor (GCD)? A: The greatest common divisor (GCD) of two or more numbers is the largest number that divides evenly into all of them. It is used to simplify fractions to their lowest terms.
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand and work with. It also ensures that the fraction is expressed in its most concise form.
Q: Can all decimals be converted to fractions? A: Yes, all terminating and repeating decimals can be converted to fractions. Non-repeating, non-terminating decimals (irrational numbers) cannot be expressed as fractions.
Q: What is the fractional equivalent of 0.875? A: The fractional equivalent of 0.875 is 7/8.
Conclusion
Converting 0.875 into a fraction involves recognizing its place value and expressing it as a fraction with a power of 10 as the denominator, followed by simplification. This process not only provides a fractional representation but also enhances understanding of the decimal's value. The result, 7/8, offers a clear and concise way to represent the same quantity, which can be particularly useful in various mathematical and real-world applications.
Now that you understand how to convert 0.875 to a fraction, put your knowledge into practice! Try converting other decimals to fractions and share your results in the comments below. Engage with fellow learners, ask questions, and deepen your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Who Is The Author Of Geronimo Stilton
Nov 28, 2025
-
What Is The Name Of Co
Nov 28, 2025
-
How To Multiply 2 Cells In Excel
Nov 28, 2025
-
What Is The Range Of Cos
Nov 28, 2025
-
Notes Of The G Major Scale
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.875 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.