What Is 0.625 In A Fraction
sonusaeterna
Nov 16, 2025 · 10 min read
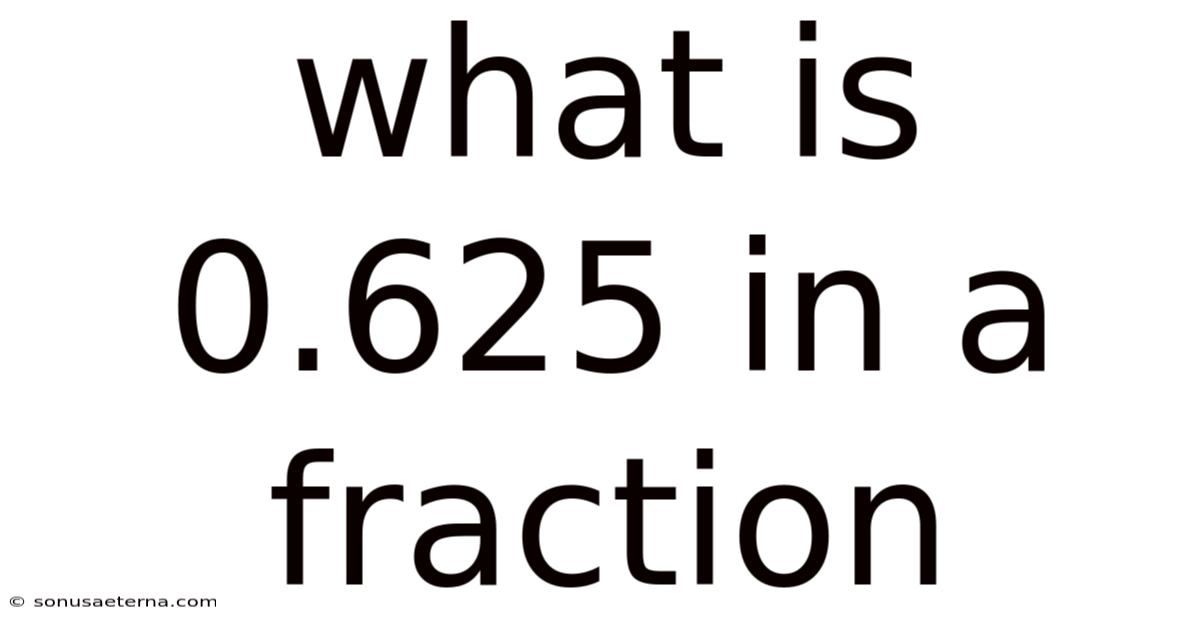
Table of Contents
The scent of freshly baked cookies wafted through the air, a warm invitation on a chilly afternoon. Little Timmy stared at a recipe, his brow furrowed in concentration. "Mom," he called out, "what does 0.625 cups of flour mean? My measuring cup only has fractions!" His mother smiled, sensing a perfect opportunity for a math lesson disguised as baking fun. Converting decimals to fractions, she knew, was a fundamental skill, a gateway to understanding proportions and ratios that would serve him well beyond the kitchen. It was more than just numbers; it was about making connections, seeing the world in terms of parts and wholes.
The world of numbers is often perceived as rigid and complex, but at its heart lies a beautiful interconnectedness. Decimals and fractions, seemingly distinct, are simply different ways of representing the same underlying reality: a portion of a whole. Understanding how to convert between them unlocks a deeper appreciation for numerical relationships and empowers us to navigate practical situations with confidence. Converting 0.625 to a fraction is a common mathematical exercise that illustrates this concept perfectly. It is a foundational skill applicable to various fields, from everyday cooking and DIY projects to advanced scientific and engineering calculations.
Main Subheading
The process of converting a decimal like 0.625 into a fraction involves understanding the place value system and applying a few simple steps. The decimal 0.625 represents a quantity less than one, specifically six hundred and twenty-five thousandths. This understanding is key to initiating the conversion. Decimals are essentially fractions with a denominator that is a power of 10 (10, 100, 1000, etc.). Recognizing this inherent relationship allows us to rewrite the decimal as a fraction and then simplify it to its lowest terms.
Think of it like this: you have a pie cut into a certain number of slices. A fraction tells you how many of those slices you have. A decimal tells you the same thing, but using a base-10 system. Converting from one to the other is simply changing the way you express the same quantity. The ability to seamlessly transition between these representations is crucial for problem-solving in many areas of life, making it a valuable skill to master. The steps required aren't complicated and, with a little practice, become second nature.
Comprehensive Overview
To fully grasp the conversion of 0.625 to a fraction, it's important to understand the underlying principles that govern decimals and fractions. This includes definitions, historical context, and practical applications.
-
Definition of a Decimal: A decimal is a number expressed in base-10 notation, using a decimal point to separate the whole number part from the fractional part. Each digit after the decimal point represents a fraction with a denominator that is a power of 10. For example, in 0.625, the '6' represents 6/10, the '2' represents 2/100, and the '5' represents 5/1000.
-
Definition of a Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of equal parts the whole is divided into.
-
Historical Context: The concept of fractions dates back to ancient civilizations, with evidence found in Egyptian and Mesopotamian mathematics. Decimals, while conceptually present in early forms, gained widespread use in the 16th century, thanks in part to the work of mathematicians like Simon Stevin. The development of both fractions and decimals was driven by the need for more precise measurement and calculation in commerce, science, and engineering.
-
The Relationship Between Decimals and Fractions: Decimals are essentially a specialized form of fractions. Any decimal can be expressed as a fraction, and vice versa. The key is to understand the place value of each digit in the decimal and use that to determine the appropriate denominator for the fraction.
-
Converting 0.625 to a Fraction: A Step-by-Step Guide:
- Identify the Place Value: In 0.625, the last digit '5' is in the thousandths place. This means the decimal represents 625 thousandths.
- Write as a Fraction: Write the decimal as a fraction with the decimal number as the numerator and the corresponding power of 10 as the denominator. In this case, 0.625 becomes 625/1000.
- Simplify the Fraction: Simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 625 and 1000 is 125. Dividing both by 125 gives us 5/8.
Therefore, 0.625 as a fraction in its simplest form is 5/8. This means that 0.625 represents five-eighths of a whole.
Trends and Latest Developments
While the basic principles of converting decimals to fractions remain constant, there are some interesting trends and developments in how these concepts are taught and applied.
-
Emphasis on Conceptual Understanding: Modern mathematics education places a greater emphasis on understanding the 'why' behind the 'how.' Instead of simply memorizing rules, students are encouraged to explore the underlying concepts and make connections between different mathematical ideas. This approach leads to a deeper and more lasting understanding.
-
Use of Visual Aids and Manipulatives: Visual aids, such as fraction bars and pie charts, are increasingly used to help students visualize fractions and decimals and understand their relationship. Manipulatives, like base-10 blocks, can also be used to represent decimals and facilitate the conversion process.
-
Technology Integration: Technology plays a significant role in modern mathematics education. Online tools and software can be used to convert decimals to fractions, simplify fractions, and explore mathematical concepts interactively. These tools can make learning more engaging and accessible.
-
Real-World Applications: Connecting mathematical concepts to real-world applications is crucial for motivating students and helping them see the relevance of what they are learning. Examples like cooking, measurement, and finance can be used to illustrate the practical applications of decimals and fractions.
-
Data-Driven Insights: In professional fields, the ability to convert between decimals and fractions is essential for data analysis and interpretation. Converting percentages (which are decimals) to fractions allows for easier comparison and manipulation of data. The rise of big data and data science has further amplified the importance of this skill.
Professional insights highlight the enduring relevance of understanding decimals and fractions. From financial analysts interpreting market trends to engineers designing structures, the ability to work comfortably with these numerical representations is essential for informed decision-making and problem-solving.
Tips and Expert Advice
Converting decimals to fractions can become second nature with practice. Here are some tips and expert advice to help you master this skill:
-
Memorize Common Decimal-Fraction Equivalents: Knowing common equivalents, such as 0.5 = 1/2, 0.25 = 1/4, and 0.75 = 3/4, can save you time and effort. You can extend this to include 0.125 = 1/8, 0.375 = 3/8, 0.625 = 5/8, and 0.875 = 7/8. These common conversions appear frequently, and memorizing them provides a solid foundation.
-
Practice Regularly: The more you practice, the more comfortable you will become with the conversion process. Work through various examples, starting with simple decimals and gradually moving on to more complex ones. Use online resources, textbooks, or worksheets to find practice problems.
-
Understand the Place Value System: A solid understanding of the place value system is crucial for converting decimals to fractions. Remember that each digit after the decimal point represents a fraction with a denominator that is a power of 10. This knowledge will guide you in correctly writing the decimal as a fraction.
-
Simplify Fractions: Always simplify the fraction to its lowest terms. This makes the fraction easier to understand and work with. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by it. There are online tools available to assist in finding the GCD if manual calculation is difficult.
-
Use Estimation to Check Your Work: After converting a decimal to a fraction, estimate the value of the fraction to see if it makes sense. For example, if you convert 0.625 to 5/8, you can estimate that 5/8 is slightly more than 1/2, which aligns with the fact that 0.625 is slightly more than 0.5. This simple check can help you catch errors.
-
Don't Be Afraid to Use Technology: Calculators and online tools can be helpful for converting decimals to fractions and simplifying fractions. However, it's important to understand the underlying process and not rely solely on technology. Use technology as a tool to check your work and speed up calculations, but always strive to understand the mathematical principles involved.
By following these tips and practicing regularly, you can develop a strong understanding of how to convert decimals to fractions and confidently apply this skill in various contexts.
FAQ
-
Q: How do I convert a decimal to a fraction if the decimal has a repeating pattern?
- A: Converting repeating decimals to fractions requires a slightly different approach involving algebra. Let x equal the repeating decimal. Multiply x by a power of 10 that shifts the repeating part to the left of the decimal point. Subtract the original equation from the new equation to eliminate the repeating part. Solve for x, which will be a fraction. For example, to convert 0.333... to a fraction, let x = 0.333.... Then 10x = 3.333.... Subtracting the first equation from the second gives 9x = 3, so x = 3/9 = 1/3.
-
Q: What is the importance of simplifying fractions after converting from a decimal?
- A: Simplifying fractions makes them easier to understand and work with. A simplified fraction represents the same value as the original fraction but with smaller numbers, which can be helpful for comparison, calculation, and communication. It presents the fraction in its most basic and understandable form.
-
Q: Can all decimals be converted to fractions?
- A: Yes, all terminating decimals (decimals that end) and repeating decimals can be converted to fractions. However, non-repeating, non-terminating decimals (irrational numbers like pi) cannot be expressed as exact fractions. They can only be approximated as fractions.
-
Q: Is there a shortcut for converting decimals to fractions?
- A: Memorizing common decimal-fraction equivalents is a useful shortcut. Also, recognizing the place value of the last digit in the decimal allows you to quickly write the decimal as a fraction with the correct denominator. For example, if the last digit is in the hundredths place, the denominator will be 100.
-
Q: What are some real-world applications of converting decimals to fractions?
- A: Converting decimals to fractions is used in cooking (adjusting recipes), measurement (converting units), finance (calculating interest rates), construction (designing structures), and science (analyzing data). Any situation that requires precise calculations and the representation of parts of a whole can benefit from this skill.
Conclusion
Converting 0.625 to a fraction, which results in 5/8, exemplifies the fundamental relationship between these two numerical representations. Understanding this conversion involves recognizing place value, applying simple division, and simplifying the resulting fraction. This seemingly basic skill has far-reaching implications, enhancing our ability to solve problems in various domains, from everyday tasks to complex professional calculations.
By mastering the art of converting decimals to fractions, you unlock a deeper understanding of mathematical concepts and equip yourself with a valuable tool for navigating the numerical world. Take the time to practice, explore, and apply this knowledge in real-world scenarios. What are some ways you can use fractions and decimals in your daily life? Share your examples in the comments below and let's continue the conversation!
Latest Posts
Latest Posts
-
What Body System Is Involved With Removing Waste
Nov 16, 2025
-
What Is A Flowering Seed Plant Called
Nov 16, 2025
-
From Where Does The Government Get Its Power
Nov 16, 2025
-
The First Family Of The United States
Nov 16, 2025
-
What Year Did Illinois Became A State
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.625 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.