Square Root Of 2 Times 2
sonusaeterna
Nov 27, 2025 · 11 min read
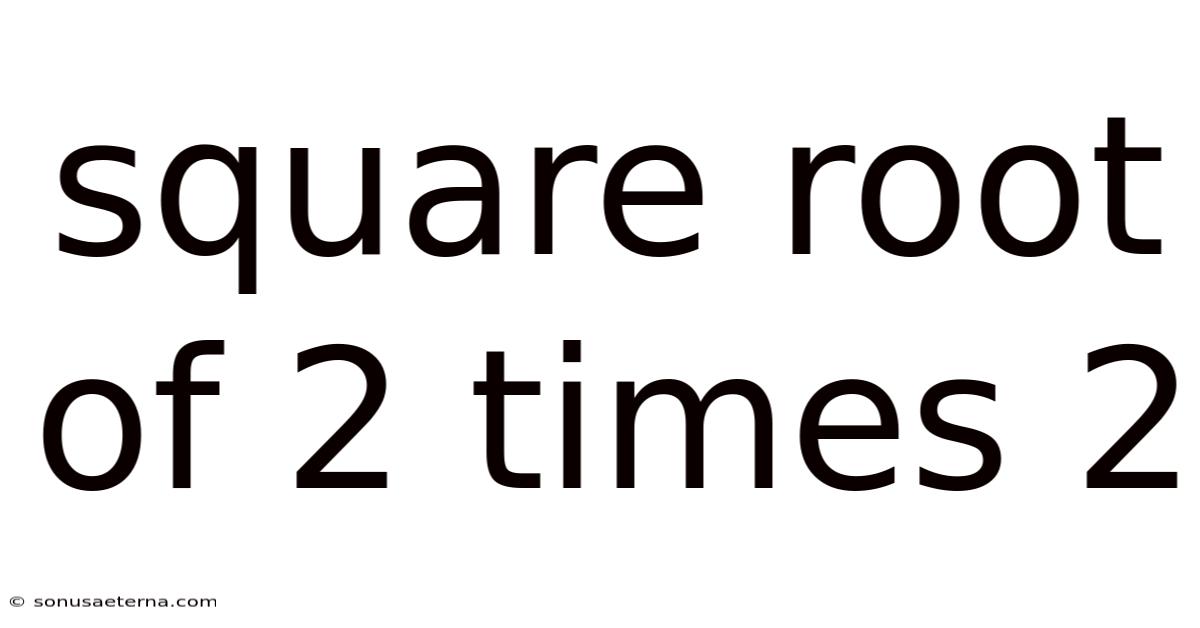
Table of Contents
Imagine you're tiling a floor, aiming for perfect squares. You have tiles that are perfect squares, but you need a way to calculate a slightly more complicated area involving the square root of 2. Or picture designing a garden, where precise measurements are crucial for the layout of pathways and flowerbeds. In both scenarios, understanding the square root of 2 and how it interacts with other numbers becomes incredibly practical. It's not just abstract math; it’s a foundational concept that pops up in the most unexpected corners of our daily lives.
Calculating areas, understanding diagonal lengths, and even designing efficient structures often hinges on a solid grasp of mathematical principles. So, when we delve into the seemingly simple expression of the square root of 2 times 2, we’re really unlocking a powerful tool that has broad applications. Let’s explore this concept to not only understand the math but also appreciate its relevance in the real world.
Understanding the Square Root of 2 Times 2
The square root of 2 times 2 can be expressed mathematically as ( 2\sqrt{2} ). This expression represents 2 multiplied by the square root of 2. At first glance, this might seem like a straightforward calculation, but it opens the door to understanding irrational numbers, algebraic manipulation, and their practical applications.
The Square Root of 2: An Irrational Number
The square root of 2, denoted as √2, is an irrational number. This means that it cannot be expressed as a simple fraction p/q, where p and q are integers. Its decimal representation is non-terminating and non-repeating, extending infinitely without any discernible pattern. Approximations are often used in calculations, but the true value remains an unending decimal.
Historically, the discovery of irrational numbers like √2 was a profound moment in mathematics. It challenged the prevailing belief that all numbers could be expressed as ratios of integers. The proof of its irrationality dates back to ancient Greece and is often attributed to Hippasus of Metapontum, a follower of Pythagoras. According to legend, the Pythagoreans considered this discovery so unsettling that they tried to suppress it, as it undermined their philosophical and mathematical foundations.
The numerical value of √2 is approximately 1.41421356237. However, it's crucial to remember that this is just an approximation. The exact value is a non-terminating, non-repeating decimal, which means it goes on infinitely without settling into a pattern. This irrationality is what makes √2 both fascinating and essential in various mathematical and real-world contexts.
Multiplying the Square Root of 2 by 2
When we multiply √2 by 2, we're essentially scaling the square root of 2. The expression ( 2\sqrt{2} ) means "two times the square root of 2." Mathematically, it’s a straightforward operation, but understanding the implications is crucial.
To calculate this, we use the approximation of √2 (1.41421356237) and multiply it by 2:
[ 2 \times \sqrt{2} \approx 2 \times 1.41421356237 \approx 2.82842712474 ]
So, ( 2\sqrt{2} ) is approximately 2.82842712474. Like √2 itself, ( 2\sqrt{2} ) is also an irrational number. Multiplying an irrational number by an integer results in another irrational number, preserving the non-terminating, non-repeating nature of the decimal representation.
The expression ( 2\sqrt{2} ) can also be represented differently using exponent rules. Recall that ( \sqrt{2} ) is equivalent to ( 2^{\frac{1}{2}} ). Therefore, ( 2\sqrt{2} ) can be written as:
[ 2 \times 2^{\frac{1}{2}} = 2^1 \times 2^{\frac{1}{2}} = 2^{1 + \frac{1}{2}} = 2^{\frac{3}{2}} ]
This representation can be particularly useful in more advanced algebraic manipulations or when dealing with exponential functions.
Practical Applications
The concept of ( 2\sqrt{2} ) appears in various fields, including geometry, engineering, and computer graphics. In geometry, it is often encountered when dealing with the diagonals and sides of squares and other related figures. For instance, if you have a square with sides of length ( \sqrt{2} ), the length of its diagonal is ( 2 ). Conversely, if you have a square where the distance from the center to one of the vertices is 1, then half the diagonal will be ( \sqrt{2} ) and the full diagonal ( 2\sqrt{2} ).
In engineering, particularly in structural design, the properties of materials and the calculation of stresses and strains often involve irrational numbers. In computer graphics, scaling and transformations of images and objects may require precise calculations involving square roots. For example, calculating the distance between points or the length of lines often involves the use of the Pythagorean theorem, which naturally leads to square roots.
Historical and Mathematical Significance
The square root of 2, and by extension ( 2\sqrt{2} ), has significant historical and mathematical importance. The discovery of irrational numbers revolutionized mathematical thinking, challenging the notion that all numbers could be expressed as ratios of integers. This discovery led to a deeper understanding of the number system and laid the foundation for more advanced mathematical concepts.
In mathematical terms, understanding and manipulating expressions involving ( 2\sqrt{2} ) provides a solid foundation for algebraic manipulations, particularly in simplifying expressions and solving equations. It also reinforces the understanding of irrational numbers and their properties, which is crucial in various branches of mathematics.
Trends and Latest Developments
In recent years, the study and application of irrational numbers like the square root of 2 have seen a resurgence, fueled by advances in computational mathematics and data analysis. As algorithms become more sophisticated, the ability to handle irrational numbers accurately is increasingly important.
Computational Mathematics
Modern computational mathematics relies heavily on approximations of irrational numbers to perform calculations that would otherwise be impossible. High-precision computing has allowed mathematicians to approximate the square root of 2 to trillions of decimal places, pushing the boundaries of computational power. This level of precision is not just an academic exercise; it has practical implications in fields such as cryptography, where the security of encryption algorithms may depend on the computational difficulty of certain mathematical problems.
Data Analysis
In data analysis, the square root of 2 is relevant in various statistical measures, such as standard deviation and root mean square (RMS) calculations. As datasets grow larger and more complex, accurate computation of these measures becomes essential. Moreover, machine learning algorithms often involve distance calculations, which frequently rely on square roots.
Educational Approaches
Educational approaches to teaching irrational numbers have also evolved. Interactive software and visual aids are now commonly used to help students grasp the concept of non-terminating, non-repeating decimals. These tools allow students to explore the properties of irrational numbers in a more intuitive and engaging way.
Popular Opinions and Misconceptions
Despite its mathematical importance, the square root of 2 is often misunderstood or overlooked in popular culture. Many people are unaware of its irrationality or its practical applications. Some common misconceptions include the belief that √2 can be expressed as a simple fraction or that it is "just a number" with no real-world relevance.
However, there is a growing appreciation for the role of mathematics in everyday life. Popular science books and documentaries often highlight the importance of mathematical concepts like the square root of 2 in fields such as physics, engineering, and computer science.
Professional Insights
From a professional perspective, understanding the square root of 2 and its properties is essential for anyone working in STEM fields. Engineers, physicists, computer scientists, and mathematicians all rely on this concept in their work. Moreover, the ability to manipulate expressions involving ( 2\sqrt{2} ) is a valuable skill in problem-solving and analytical thinking.
As technology continues to advance, the importance of mathematical literacy will only grow. Professionals who have a solid understanding of fundamental concepts like the square root of 2 will be better equipped to tackle the challenges of the future.
Tips and Expert Advice
Mastering the concept of the square root of 2 times 2 involves more than just memorizing its approximate value. It requires a deep understanding of irrational numbers, algebraic manipulation, and practical applications. Here are some tips and expert advice to help you build a solid foundation:
Tip 1: Visualize Geometric Representations
One of the best ways to understand the square root of 2 is to visualize its geometric representation. Consider a square with sides of length 1. According to the Pythagorean theorem, the length of the diagonal is ( \sqrt{1^2 + 1^2} = \sqrt{2} ). This visual representation helps to connect the abstract concept of an irrational number with a concrete geometric object.
Similarly, consider a square with sides of length ( \sqrt{2} ). The length of its diagonal is ( \sqrt{(\sqrt{2})^2 + (\sqrt{2})^2} = \sqrt{2 + 2} = \sqrt{4} = 2 ). If you then were to double the side length of the original square to 2 times √2, you can also consider the properties of similar figures to extrapolate other measurements. This exercise reinforces the relationship between the square root of 2 and geometric shapes.
Tip 2: Practice Algebraic Manipulation
Algebraic manipulation is essential for simplifying expressions involving ( 2\sqrt{2} ). Practice simplifying expressions and solving equations that involve square roots. For example, try simplifying expressions like ( (2\sqrt{2})^2 ) or ( \frac{4}{2\sqrt{2}} ).
Also, try solving equations that involve ( 2\sqrt{2} ). For instance, if ( x = 2\sqrt{2} ), find the value of ( x^2 - 8 ). These exercises will help you to develop your algebraic skills and deepen your understanding of irrational numbers.
Tip 3: Explore Real-World Applications
To appreciate the practical relevance of ( 2\sqrt{2} ), explore its real-world applications. Look for examples in geometry, engineering, computer graphics, and other fields. For instance, research how the square root of 2 is used in the design of buildings, bridges, and other structures.
Also, consider how it is used in computer algorithms for image processing and computer-aided design. Understanding these applications will make the concept more meaningful and memorable.
Tip 4: Use Computational Tools
Modern computational tools can be a valuable resource for exploring the properties of ( 2\sqrt{2} ). Use calculators, computer algebra systems, and online resources to approximate its value to a high degree of precision.
Also, use these tools to perform calculations and solve equations that involve ( 2\sqrt{2} ). These tools can help you to verify your work and gain a deeper understanding of the concept.
Tip 5: Study Historical Context
Finally, take the time to study the historical context of the square root of 2. Learn about the discovery of irrational numbers and the challenges it posed to ancient mathematicians.
Understanding the historical significance of ( 2\sqrt{2} ) will give you a greater appreciation for its importance and its place in the history of mathematics. It will also help you to connect with the mathematical community and see yourself as part of a long and rich tradition of intellectual inquiry.
FAQ
Q: What is the approximate value of ( 2\sqrt{2} )? A: The approximate value of ( 2\sqrt{2} ) is 2.82842712474.
Q: Is ( 2\sqrt{2} ) a rational or irrational number? A: ( 2\sqrt{2} ) is an irrational number.
Q: Can ( 2\sqrt{2} ) be expressed as a fraction? A: No, ( 2\sqrt{2} ) cannot be expressed as a simple fraction p/q, where p and q are integers.
Q: How is ( 2\sqrt{2} ) used in geometry? A: ( 2\sqrt{2} ) is used in geometry to calculate the length of diagonals and sides of squares and other related figures.
Q: How can I simplify expressions involving ( 2\sqrt{2} )? A: To simplify expressions involving ( 2\sqrt{2} ), use algebraic manipulation techniques, such as factoring, combining like terms, and applying exponent rules.
Q: What is the historical significance of ( 2\sqrt{2} )? A: The square root of 2, and by extension ( 2\sqrt{2} ), has significant historical importance because its discovery as an irrational number challenged the prevailing belief that all numbers could be expressed as ratios of integers.
Q: Where can I find more information about ( 2\sqrt{2} )? A: You can find more information about ( 2\sqrt{2} ) in mathematics textbooks, online resources, and scientific articles.
Conclusion
In summary, understanding the square root of 2 times 2, or ( 2\sqrt{2} ), is more than just a mathematical exercise. It's an exploration of irrational numbers, algebraic manipulation, and their practical applications in various fields. From geometry to engineering to computer graphics, the concept of ( 2\sqrt{2} ) plays a crucial role in problem-solving and analytical thinking.
By visualizing geometric representations, practicing algebraic manipulation, exploring real-world applications, using computational tools, and studying the historical context, you can build a solid foundation in this important mathematical concept.
Now, take the next step. Try applying these principles to solve real-world problems, explore advanced mathematical concepts, or simply share your newfound knowledge with others. Engage with the material, ask questions, and continue to deepen your understanding of the square root of 2 times 2. Your mathematical journey has just begun!
Latest Posts
Latest Posts
-
How Do You Construct An Altitude Of A Triangle
Nov 27, 2025
-
What Is Local Maximum On A Graph
Nov 27, 2025
-
How Long Is The Chesapeake Bay Tunnel
Nov 27, 2025
-
How Fast Can The Fastest Bird Fly
Nov 27, 2025
-
Longest Mountain Range In North America
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.