Measure Of An Inscribed Angle Theorem
sonusaeterna
Nov 14, 2025 · 13 min read
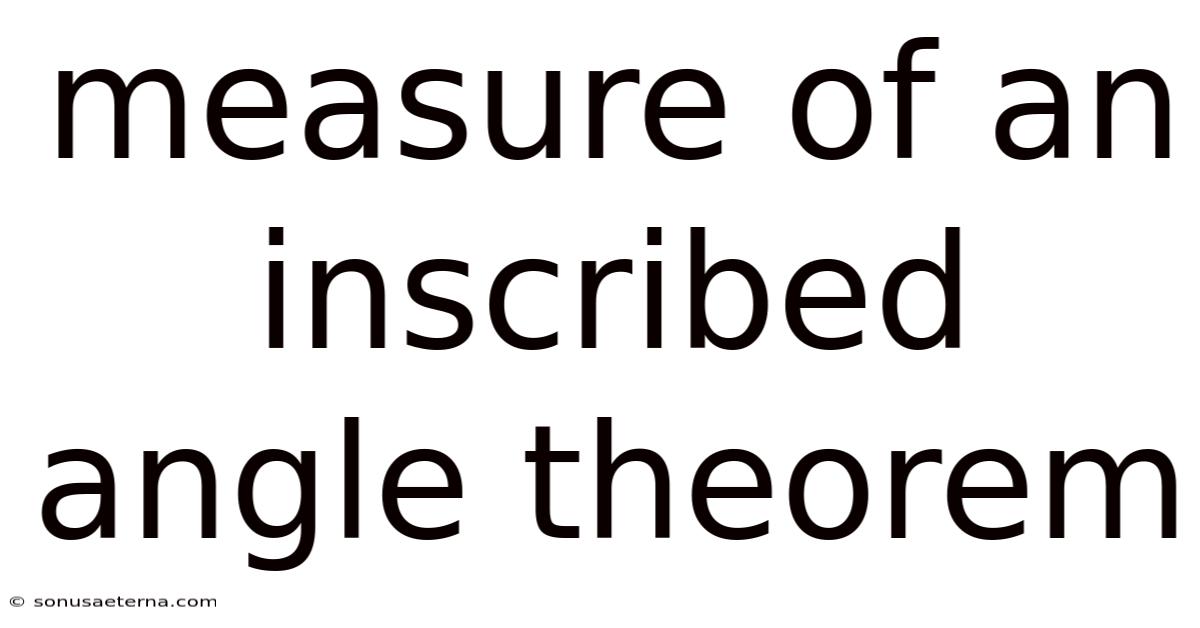
Table of Contents
Imagine you're gazing at a perfectly round pizza, sliced into neat pieces. Each slice forms an angle, and the crust creates a beautiful arc. Now, picture yourself picking a slice, not from the center, but from a point on the edge of the pizza. The angle formed by your slice, with its point resting on the circumference, is an inscribed angle. This seemingly simple observation unlocks a world of geometric relationships, especially when we start thinking about how the size of that angle relates to the arc it carves out on the pizza's crust.
In geometry, the relationship between these angles and arcs isn't arbitrary—it’s governed by a precise rule known as the inscribed angle theorem. This theorem isn't just some abstract concept; it’s a fundamental principle that elegantly connects angles and circles, providing a foundation for understanding more complex geometric figures and proofs. Whether you're designing a bridge, mapping the stars, or simply solving a puzzle, understanding the inscribed angle theorem unlocks a powerful tool for visualising and calculating geometric relationships. Let’s delve into the heart of this theorem, exploring its nuances, applications, and why it remains a cornerstone of geometric understanding.
Main Subheading
The inscribed angle theorem is a gem in the world of geometry, elegantly connecting angles and arcs within a circle. It serves as a cornerstone for understanding various geometric relationships and is an indispensable tool for solving problems involving circles. At its core, the theorem defines a specific relationship between an angle whose vertex lies on the circle's circumference and the arc it intercepts.
Understanding the context and background of the inscribed angle theorem helps to appreciate its significance. Circles have been a subject of fascination and mathematical inquiry for millennia, appearing in art, architecture, and countless natural phenomena. As mathematicians began to explore the properties of circles more deeply, they discovered that angles formed within a circle are intimately related to the arcs they cut off. This revelation led to the formalization of the inscribed angle theorem, which provides a precise way to measure these relationships. The theorem is not just an isolated concept; it builds upon earlier geometric principles and lays the groundwork for more advanced topics.
Comprehensive Overview
To fully grasp the inscribed angle theorem, it’s essential to define its key components and understand the foundational concepts that underpin it. An inscribed angle is an angle formed by two chords in a circle that have a common endpoint. This common endpoint forms the vertex of the angle, and it lies on the circumference of the circle. The arc intercepted by the inscribed angle is the portion of the circle's circumference that lies within the angle’s "arms."
Formally, the inscribed angle theorem states: The measure of an inscribed angle is half the measure of its intercepted arc. Mathematically, this can be expressed as:
Inscribed Angle = 1/2 * Intercepted Arc
To appreciate the theorem's significance, let's consider its historical roots. The study of circles dates back to ancient civilizations, including the Babylonians, Egyptians, and Greeks. Early mathematicians observed empirical relationships between angles and arcs in circles, but it was the Greeks who rigorously formalized these observations into theorems. Euclid, in his seminal work Elements, laid down many of the foundational principles of geometry, including those related to circles. While Euclid didn't explicitly state the inscribed angle theorem in its modern form, his work contains elements that implicitly point towards it. Over centuries, mathematicians refined and extended these ideas, eventually leading to the precise formulation of the inscribed angle theorem as we know it today.
To truly understand the inscribed angle theorem, it is important to consider its scientific foundations. The theorem is rooted in basic geometric principles, such as the properties of chords, arcs, and central angles. A central angle is an angle whose vertex is at the center of the circle. There is a direct relationship between a central angle and the arc it intercepts: the measure of the central angle is equal to the measure of the intercepted arc. The inscribed angle theorem essentially connects the inscribed angle to the central angle, demonstrating that the inscribed angle is always half the central angle that intercepts the same arc.
The proof of the inscribed angle theorem involves several cases, each addressing a different position of the inscribed angle relative to the center of the circle. The primary cases include:
- The center of the circle lies on one arm of the inscribed angle: In this case, the proof involves recognizing that the triangle formed by the radius, the chord, and the line connecting the center to the vertex of the inscribed angle is an isosceles triangle. This allows us to relate the angles and deduce the relationship between the inscribed angle and the central angle.
- The center of the circle lies inside the inscribed angle: In this case, the inscribed angle can be divided into two smaller inscribed angles, each of which falls under the first case. By applying the theorem to each smaller angle and then summing the results, we can prove the theorem for the entire inscribed angle.
- The center of the circle lies outside the inscribed angle: In this scenario, the inscribed angle is the difference between two inscribed angles, each of which falls under the first case. By applying the theorem to each smaller angle and then subtracting the results, we can prove the theorem for the entire inscribed angle.
Understanding these proofs not only reinforces the validity of the inscribed angle theorem but also provides valuable insights into the logical rigor of geometric reasoning. The theorem serves as a building block for proving other theorems and solving complex geometric problems.
Beyond its theoretical significance, the inscribed angle theorem has practical applications in various fields. In architecture and engineering, the theorem can be used to design structures with circular elements, ensuring precise measurements and optimal stability. In navigation, it helps in calculating distances and bearings based on angles observed from a point on the Earth's surface. Even in computer graphics and game development, the theorem is used to create realistic and accurate representations of circular objects and movements.
Trends and Latest Developments
In recent years, the inscribed angle theorem has seen a resurgence in interest, driven by advancements in technology and new approaches to mathematical education. One notable trend is the use of dynamic geometry software (DGS) to visually demonstrate and explore the theorem. Programs like GeoGebra and Desmos allow students to manipulate geometric figures in real-time, making the abstract concepts of angles and arcs more tangible and intuitive. By constructing circles, chords, and inscribed angles, students can observe firsthand how the measure of the inscribed angle changes as the intercepted arc is altered. This interactive approach not only enhances understanding but also fosters a deeper appreciation for the theorem's elegance and power.
Another trend is the integration of the inscribed angle theorem into interdisciplinary projects that connect mathematics with other subjects. For example, students might use the theorem to analyze the design of historical buildings with circular features or to model the trajectory of a projectile moving along a circular path. These projects encourage students to apply their mathematical knowledge in real-world contexts, making learning more engaging and relevant.
Moreover, researchers are exploring new applications of the inscribed angle theorem in fields such as cryptography and data analysis. While these applications are still in their early stages, they highlight the theorem's potential to contribute to cutting-edge technologies. For instance, the theorem could be used to develop algorithms for secure communication or to analyze patterns in circular data sets.
Professional insights into the inscribed angle theorem often emphasize the importance of conceptual understanding over rote memorization. Experienced educators stress that students should not only be able to state the theorem but also understand its underlying principles and be able to apply it in various problem-solving scenarios. This requires a shift away from traditional lecture-based teaching towards more active and inquiry-based approaches.
Furthermore, experts highlight the connections between the inscribed angle theorem and other fundamental concepts in geometry. Understanding these connections can help students develop a more cohesive and integrated view of mathematics. For example, the inscribed angle theorem is closely related to the central angle theorem, the properties of cyclic quadrilaterals, and the concept of similarity. By exploring these relationships, students can gain a deeper appreciation for the interconnectedness of mathematical ideas.
Tips and Expert Advice
Mastering the inscribed angle theorem involves more than just memorizing the formula; it requires understanding its nuances and applying it effectively in problem-solving. Here are some tips and expert advice to help you develop a strong grasp of the theorem:
-
Visualize the Theorem: The inscribed angle theorem is inherently visual, so make use of diagrams and drawings to understand the relationship between the inscribed angle and its intercepted arc. Draw various circles with different inscribed angles and their corresponding arcs. Notice how the measure of the inscribed angle changes as the size of the arc changes. This visual exercise will solidify your understanding of the theorem and make it easier to apply in problem-solving. Try using dynamic geometry software to create interactive visualizations that allow you to manipulate the figures and observe the relationships in real-time.
-
Practice with Different Cases: As mentioned earlier, the proof of the inscribed angle theorem involves several cases, each addressing a different position of the inscribed angle relative to the center of the circle. To fully understand the theorem, practice solving problems that involve each of these cases. This will help you develop a flexible and adaptable approach to problem-solving. For example, try solving problems where the center of the circle lies on one arm of the inscribed angle, inside the inscribed angle, and outside the inscribed angle.
-
Relate the Theorem to Other Concepts: The inscribed angle theorem is closely related to other fundamental concepts in geometry, such as the central angle theorem, the properties of cyclic quadrilaterals, and the concept of similarity. Understanding these connections will help you develop a more cohesive and integrated view of mathematics. For example, try solving problems that involve both the inscribed angle theorem and the central angle theorem. This will help you see how the two theorems are related and how they can be used together to solve more complex problems.
-
Break Down Complex Problems: Many geometry problems involve multiple steps and require you to apply several theorems and concepts. When faced with a complex problem, break it down into smaller, more manageable parts. Identify the key information, draw a clear diagram, and apply the inscribed angle theorem to the relevant parts of the problem. Then, use other geometric principles to connect the pieces and arrive at the solution. This step-by-step approach will make complex problems less daunting and more accessible.
-
Use Real-World Examples: The inscribed angle theorem has practical applications in various fields, such as architecture, engineering, and navigation. To make the theorem more relevant and engaging, try exploring real-world examples of its use. For instance, you could analyze the design of a building with circular features or investigate how the theorem is used in GPS technology. This will help you see the theorem in action and appreciate its practical significance.
-
Check Your Work: When solving geometry problems, always check your work to ensure that your answers are accurate and consistent. Double-check your calculations, review your diagrams, and make sure that your reasoning is sound. If possible, try solving the problem using a different approach to verify your answer. This will help you catch any errors and develop a more confident and reliable problem-solving technique.
-
Teach Someone Else: One of the best ways to solidify your understanding of a concept is to teach it to someone else. Try explaining the inscribed angle theorem to a friend or family member. This will force you to organize your thoughts, clarify your understanding, and identify any gaps in your knowledge. In addition, teaching can be a rewarding experience that reinforces your own learning.
FAQ
Q: What exactly is an inscribed angle?
A: An inscribed angle is an angle formed by two chords in a circle that share a common endpoint, with the vertex of the angle lying on the circle's circumference.
Q: How does the inscribed angle theorem relate to the central angle theorem?
A: The inscribed angle theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. The central angle theorem states that the measure of a central angle is equal to the measure of its intercepted arc. Therefore, the inscribed angle is half the central angle that intercepts the same arc.
Q: Can the inscribed angle theorem be used to prove other geometric theorems?
A: Yes, the inscribed angle theorem is a fundamental building block for proving other theorems related to circles, such as the properties of cyclic quadrilaterals and the intersecting chords theorem.
Q: What if the center of the circle lies outside the inscribed angle? Does the theorem still apply?
A: Yes, the inscribed angle theorem applies regardless of the position of the center of the circle relative to the inscribed angle. The proof involves considering different cases, but the relationship between the inscribed angle and its intercepted arc remains the same.
Q: How can I use the inscribed angle theorem in real-world applications?
A: The inscribed angle theorem has applications in various fields, such as architecture, engineering, navigation, and computer graphics. It can be used to calculate distances, design structures with circular elements, and create realistic representations of circular objects.
Conclusion
The inscribed angle theorem is a powerful tool for understanding the relationships between angles and arcs in circles. It elegantly connects angles whose vertices lie on the circle's circumference to the arcs they intercept, providing a foundation for solving a wide range of geometric problems. From its historical roots in ancient geometry to its modern applications in technology and design, the inscribed angle theorem continues to be a relevant and valuable concept.
By visualizing the theorem, practicing with different cases, and relating it to other geometric principles, you can develop a strong grasp of this fundamental concept. Remember to break down complex problems, use real-world examples, and always check your work. With practice and dedication, you can master the inscribed angle theorem and unlock its full potential.
Now that you have a comprehensive understanding of the inscribed angle theorem, take the next step and apply your knowledge to solve challenging geometry problems. Explore real-world applications of the theorem, and share your insights with others. By actively engaging with the material, you can deepen your understanding and appreciate the beauty and power of mathematics. Share this article with fellow learners, and let’s explore the world of geometry together!
Latest Posts
Latest Posts
-
What Does A Small Snapping Turtle Look Like
Nov 14, 2025
-
How Many Turns Of The Krebs Cycle Per Glucose
Nov 14, 2025
-
Difference Between An Ac And Dc Generator
Nov 14, 2025
-
Who Was Antinous In The Odyssey
Nov 14, 2025
-
How To Say Girlfriend In French
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about Measure Of An Inscribed Angle Theorem . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.