Is 2 3 Cup Less Than 1 2 Cup
sonusaeterna
Nov 15, 2025 · 13 min read
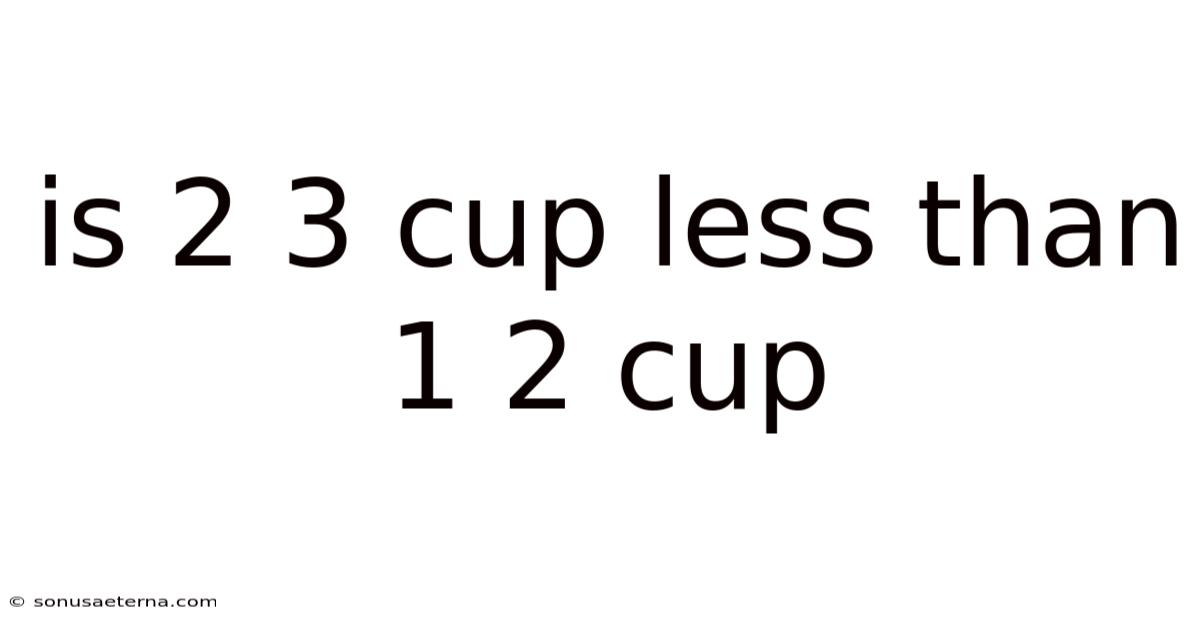
Table of Contents
Imagine you're baking your favorite chocolate chip cookies. The recipe calls for 1/2 cup of butter, but you find yourself staring at a measuring cup filled with 2/3 cup of sugar. A quick substitution thought pops into your head, and now you are wondering if 2/3 cup is less than 1/2 cup.
We often encounter fractions in our daily lives, from cooking and baking to measuring distances and managing time. Understanding how to compare fractions is a fundamental skill. When fractions have different numerators and denominators, figuring out which one is larger can be tricky. So, is 2/3 cup less than 1/2 cup? Let's dive into the world of fractions to find out.
Main Subheading
At first glance, determining whether 2/3 is less than 1/2 might seem straightforward, but it requires a bit of understanding about what fractions truly represent. Fractions are used to represent parts of a whole, and comparing them involves understanding how these parts relate to each other. The difficulty arises because the denominators are different. A denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we have. To compare fractions accurately, we need to find a common ground, usually by finding a common denominator. This allows us to compare "apples to apples," making it clear which fraction represents a larger portion of the whole.
Without a common denominator, we're essentially trying to compare different sized slices of a pie without knowing how big the pie originally was. For example, if you cut a pie into three slices and take two (2/3), and someone else cuts a similar pie into two slices and takes one (1/2), it's not immediately obvious who has more pie. The trick is to re-slice both pies into the same number of slices, which is what finding a common denominator achieves. Once the denominators are the same, you can simply compare the numerators to see which fraction is larger or smaller. This method not only helps in academic settings but also in practical, everyday situations where understanding proportions is essential.
Comprehensive Overview
To understand whether 2/3 cup is less than 1/2 cup, we need to delve into the basics of fractions and how to compare them. A fraction represents a part of a whole. It consists of two numbers: the numerator (the number on top) and the denominator (the number on the bottom). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering.
For example, in the fraction 1/2, the denominator 2 tells us that the whole is divided into two equal parts, and the numerator 1 tells us that we are considering one of those parts. Similarly, in the fraction 2/3, the denominator 3 tells us that the whole is divided into three equal parts, and the numerator 2 tells us that we are considering two of those parts.
Definition of Fractions
A fraction is a numerical quantity that is not a whole number. It is written as a ratio of two numbers, the numerator and the denominator. The denominator cannot be zero because division by zero is undefined. Fractions can represent various concepts, such as parts of a whole, ratios, or probabilities.
Scientific Foundation
The concept of fractions has its roots in ancient mathematics. Egyptians and Babylonians used fractions extensively in their calculations related to land measurement, trade, and construction. The Egyptians, for example, used unit fractions (fractions with a numerator of 1) and expressed other fractions as sums of unit fractions. The Babylonians used sexagesimal fractions (fractions with a denominator of 60) in their astronomical calculations.
History of Fractions
The use of fractions dates back to ancient civilizations. Egyptians used fractions as early as 3000 BC, and the Babylonians developed a sophisticated system of fractions based on the number 60. The concept of representing fractions as we do today, with a numerator and a denominator separated by a line, evolved over time. Indian mathematicians made significant contributions to the understanding and manipulation of fractions, and their methods were later adopted by Arab scholars and transmitted to Europe.
Essential Concepts
To compare fractions, we need to understand the following essential concepts:
- Common Denominator: To compare fractions accurately, they must have the same denominator. This means that the whole is divided into the same number of equal parts for both fractions.
- Equivalent Fractions: These are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions because they both represent half of a whole.
- Simplifying Fractions: Simplifying a fraction means reducing it to its simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, the fraction 4/8 can be simplified to 1/2 by dividing both 4 and 8 by their GCD, which is 4.
Comparing Fractions
There are several methods to compare fractions:
-
Finding a Common Denominator: This is the most common method. To compare 1/2 and 2/3, we need to find a common denominator. The least common multiple (LCM) of 2 and 3 is 6. So, we convert both fractions to have a denominator of 6:
- 1/2 = (1 * 3) / (2 * 3) = 3/6
- 2/3 = (2 * 2) / (3 * 2) = 4/6 Now that both fractions have the same denominator, we can compare their numerators. Since 3 < 4, we can conclude that 3/6 < 4/6, which means 1/2 < 2/3.
-
Cross-Multiplication: This method involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results. For example, to compare 1/2 and 2/3:
- 1/2 vs. 2/3
- 1 * 3 = 3
- 2 * 2 = 4 Since 3 < 4, we can conclude that 1/2 < 2/3.
-
Converting to Decimals: Another way to compare fractions is to convert them to decimals and then compare the decimal values. For example:
- 1/2 = 0.5
- 2/3 ≈ 0.67 Since 0.5 < 0.67, we can conclude that 1/2 < 2/3.
Using any of these methods, it becomes clear that 2/3 is greater than 1/2. So, 2/3 cup is not less than 1/2 cup. In fact, it's more.
Trends and Latest Developments
In recent years, there has been an increased emphasis on mathematical literacy and numeracy skills, driven by the recognition that a strong foundation in mathematics is essential for success in various fields. Educational research consistently highlights the importance of understanding fractions as a building block for more advanced mathematical concepts, such as algebra and calculus. This has led to innovative teaching methods and resources aimed at making fractions more accessible and engaging for students.
One notable trend is the use of visual aids and manipulatives to help students understand fractions conceptually. Tools like fraction bars, fraction circles, and interactive online simulations allow students to physically and visually represent fractions, making it easier to grasp the relationships between numerators and denominators. These hands-on approaches have been shown to improve students' understanding and retention of fraction concepts.
Another trend is the integration of real-world applications of fractions into mathematics curricula. Instead of just learning abstract rules and procedures, students are encouraged to explore how fractions are used in everyday contexts, such as cooking, baking, measuring, and financial planning. By connecting fractions to real-life scenarios, students can see the relevance and practicality of what they are learning, which can increase their motivation and engagement.
Data from educational assessments consistently show that students struggle with fractions, particularly when it comes to comparing and performing operations with fractions. However, research also indicates that targeted interventions and instructional strategies can significantly improve students' understanding of fractions. For example, studies have found that providing students with explicit instruction on common misconceptions about fractions, such as the belief that larger denominators always mean larger fractions, can help them overcome these misconceptions and develop a more accurate understanding.
Professional insights from mathematics educators emphasize the importance of building a strong conceptual foundation in fractions before moving on to more advanced topics. Rushing through fraction concepts without ensuring that students have a solid understanding can lead to difficulties later on. Instead, educators should focus on helping students develop a deep understanding of fractions, which will enable them to apply these concepts flexibly and confidently in a variety of contexts.
Tips and Expert Advice
Understanding and comparing fractions can be made easier with the right strategies. Here are some practical tips and expert advice to help you master this essential mathematical skill:
-
Use Visual Aids: Visual aids can be incredibly helpful for understanding fractions, especially for those who are new to the concept. Tools like fraction bars, circles, and diagrams provide a concrete way to see and compare fractions. For example, if you're trying to compare 1/2 and 2/3, draw two circles of the same size. Divide one circle into two equal parts and shade one part to represent 1/2. Then, divide the other circle into three equal parts and shade two parts to represent 2/3. By visually comparing the shaded areas, you can easily see that 2/3 is larger than 1/2.
Visual aids are not just for beginners; they can also be useful for more complex problems. When dealing with mixed numbers or improper fractions, drawing diagrams can help you break down the problem into smaller, more manageable parts. Additionally, there are many online resources and apps that offer interactive fraction models, allowing you to manipulate fractions and see the results in real time.
-
Find Common Denominators: As mentioned earlier, finding a common denominator is crucial for comparing fractions accurately. The least common multiple (LCM) of the denominators is the easiest way to find a common denominator. To find the LCM, list the multiples of each denominator until you find a common multiple. For example, to compare 1/4 and 3/10, list the multiples of 4 and 10:
- Multiples of 4: 4, 8, 12, 16, 20, 24, ...
- Multiples of 10: 10, 20, 30, 40, ... The LCM of 4 and 10 is 20.
Once you find the common denominator, convert each fraction to an equivalent fraction with that denominator. In this case:
- 1/4 = (1 * 5) / (4 * 5) = 5/20
- 3/10 = (3 * 2) / (10 * 2) = 6/20 Now that both fractions have the same denominator, you can easily compare them. Since 5/20 < 6/20, we can conclude that 1/4 < 3/10.
-
Practice Regularly: Like any skill, mastering fractions requires practice. The more you work with fractions, the more comfortable you will become with comparing them. Start with simple fractions and gradually work your way up to more complex problems. Online resources, textbooks, and worksheets can provide you with plenty of practice opportunities.
Don't just focus on rote memorization of rules and procedures. Instead, try to understand the underlying concepts and principles. This will help you develop a deeper understanding of fractions and enable you to apply them in a variety of contexts. Additionally, look for real-world applications of fractions in your daily life. This will make learning fractions more engaging and meaningful.
-
Use Benchmarks: Benchmarks are common fractions that can be used as reference points when comparing other fractions. Some common benchmarks include 0, 1/4, 1/3, 1/2, 2/3, 3/4, and 1. When comparing a fraction to a benchmark, ask yourself whether the fraction is closer to 0, 1/2, or 1. For example, if you're trying to compare 3/8 and 2/5, you can use 1/2 as a benchmark.
3/8 is slightly less than 1/2 (since 4/8 = 1/2), and 2/5 is slightly less than 1/2 (since 2.5/5 = 1/2). However, 3/8 is closer to 1/2 than 2/5, so 3/8 is slightly larger than 2/5. Using benchmarks can help you quickly estimate the relative sizes of fractions without having to find a common denominator.
-
Understand the Numerator and Denominator: Make sure you have a solid understanding of what the numerator and denominator represent. The denominator tells you how many equal parts the whole is divided into, and the numerator tells you how many of those parts you are considering. Understanding this relationship is essential for comparing fractions accurately.
For example, if you're comparing 1/3 and 1/4, you need to understand that 1/3 means one part out of three equal parts, and 1/4 means one part out of four equal parts. Since the whole is divided into fewer parts in 1/3, each part is larger, so 1/3 is greater than 1/4. By understanding the meaning of the numerator and denominator, you can develop a more intuitive sense of how fractions relate to each other.
FAQ
Q: What is a fraction? A: A fraction represents a part of a whole and is expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number).
Q: Why do we need to find a common denominator to compare fractions? A: A common denominator allows us to compare fractions with the same sized "slices," making it easy to determine which fraction represents a larger portion of the whole.
Q: How do you find a common denominator? A: Find the least common multiple (LCM) of the denominators of the fractions you want to compare. Then, convert each fraction to an equivalent fraction with the LCM as the new denominator.
Q: What is cross-multiplication? A: Cross-multiplication is a method to compare two fractions by multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results.
Q: Can you use decimals to compare fractions? A: Yes, you can convert fractions to decimals by dividing the numerator by the denominator and then compare the decimal values.
Q: What are equivalent fractions? A: Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 and 2/4).
Conclusion
In summary, understanding how to compare fractions is crucial for various everyday tasks, from cooking to managing finances. When comparing 2/3 cup and 1/2 cup, we've learned that 2/3 is actually greater than 1/2. By using methods like finding a common denominator, cross-multiplication, or converting to decimals, we can accurately determine the relative sizes of fractions. These skills are not only valuable in academic settings but also in practical, real-world situations.
Ready to put your fraction skills to the test? Try comparing different fractions in your daily life, whether it's while cooking, measuring, or even planning your day. Share your experiences and insights in the comments below! Let's continue to build our understanding of fractions together.
Latest Posts
Latest Posts
-
How Long Is The Ap Psych Exam
Nov 15, 2025
-
How Do You Say Good Evening In German
Nov 15, 2025
-
How Can I Get Access To The Mls Database
Nov 15, 2025
-
Why Did The Explorer Come To Texas
Nov 15, 2025
-
How Can I Get A Series 7 License
Nov 15, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Cup Less Than 1 2 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.