Half Of 1 And 3/4 Cups
sonusaeterna
Nov 18, 2025 · 9 min read
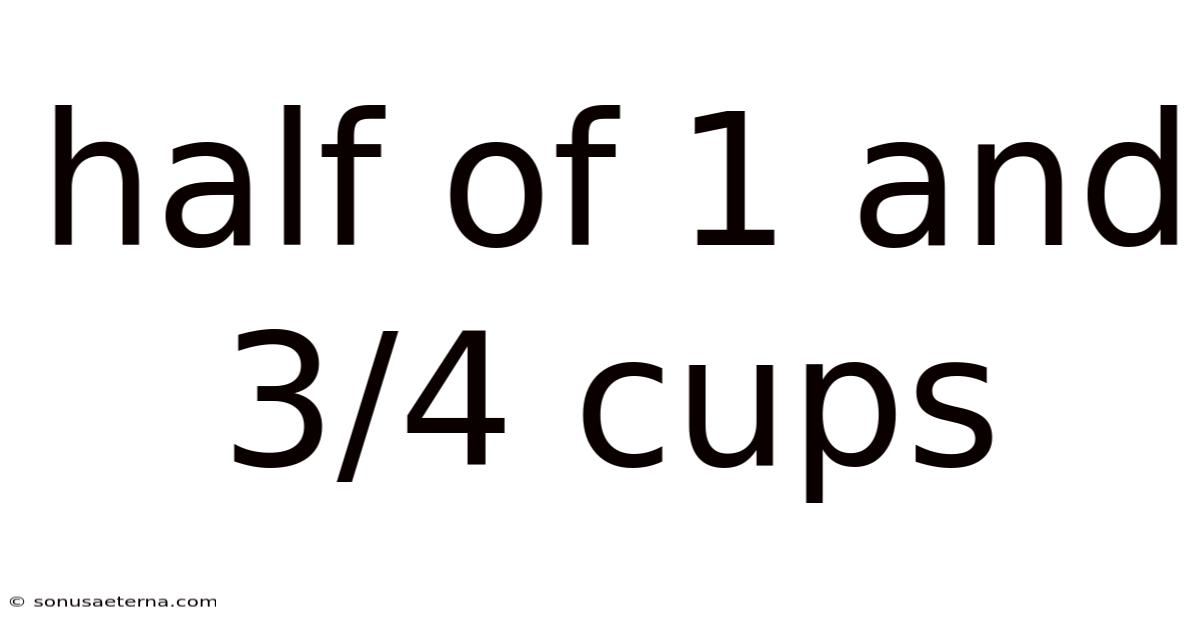
Table of Contents
Imagine you're in the middle of baking your favorite chocolate chip cookies, the kind that makes your kitchen smell heavenly and brings smiles to everyone's faces. You grab your measuring cups, ready to combine the ingredients, but the recipe calls for "half of 1 and 3/4 cups" of flour. Suddenly, you pause. What exactly is half of 1 and 3/4 cups? It's a common kitchen conundrum, but don't worry, it's easier to solve than you might think.
Figuring out half of 1 and 3/4 cups is not just a kitchen skill; it's a practical math problem that pops up in various everyday situations. Whether you're scaling down a recipe, dividing ingredients for a science experiment, or even splitting resources evenly, knowing how to find half of a mixed number is incredibly useful. This article will break down the process step-by-step, providing you with clear explanations, helpful tips, and real-world examples to master this essential skill. Let's dive in and make sure your measurements are always on point.
Main Subheading
To understand half of 1 and 3/4 cups, we need to first grasp the basic concepts of fractions and mixed numbers. This involves understanding what fractions represent, how they are structured, and how mixed numbers combine whole numbers and fractions. When faced with finding half of a mixed number like 1 and 3/4, it's not as simple as just halving the whole number and the fraction separately. Instead, a more systematic approach is required to ensure accuracy.
Think of it this way: 1 and 3/4 cups is a quantity that lies between one full cup and two full cups. Finding half of this amount means we are looking for a value that is exactly in the middle of zero and 1 and 3/4 cups. This sort of problem often arises in cooking, baking, and various forms of measurement, highlighting the importance of mastering this skill. Whether you are a seasoned chef or a novice baker, understanding how to halve mixed numbers is essential for precise and consistent results.
Comprehensive Overview
Understanding Fractions and Mixed Numbers
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a total of 4 equal parts.
A mixed number is a combination of a whole number and a fraction. For instance, 1 and 3/4 is a mixed number, where 1 is the whole number and 3/4 is the fraction. Mixed numbers are used to represent quantities greater than one whole unit. In our case, 1 and 3/4 cups means we have one full cup plus three-quarters of another cup.
Converting Mixed Numbers to Improper Fractions
To find half of a mixed number, it’s often easiest to convert it into an improper fraction. An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4). Here's how to convert 1 and 3/4 into an improper fraction:
- Multiply the whole number (1) by the denominator of the fraction (4): 1 * 4 = 4.
- Add the result to the numerator (3): 4 + 3 = 7.
- Place the sum over the original denominator (4): 7/4.
So, 1 and 3/4 is equal to 7/4.
Dividing Fractions
Dividing a fraction by a whole number is equivalent to multiplying the fraction by the reciprocal of that whole number. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 2 is 1/2.
To find half of 7/4, you multiply 7/4 by 1/2:
(7/4) * (1/2) = 7/8
Therefore, half of 7/4 (or 1 and 3/4) is 7/8.
The Logic Behind It
Why does this method work? When we convert a mixed number to an improper fraction, we are expressing the entire quantity in terms of the smallest unit (in this case, quarters). By multiplying by 1/2, we are finding half of each of those units.
For example, 1 and 3/4 cups is the same as 7 quarters of a cup. Taking half of each quarter results in each quarter being divided into two, effectively making eighths. Since we had 7 quarters, we now have 7 eighths, hence 7/8.
Real-World Applications and History
The concept of fractions and mixed numbers dates back to ancient civilizations. Egyptians and Babylonians used fractions extensively for land measurement, trade, and construction. The Rhind Papyrus, an ancient Egyptian mathematical document, contains numerous problems involving fractions.
In modern times, understanding fractions and mixed numbers is crucial in various fields, including:
- Cooking and Baking: Recipes often require precise measurements using fractions.
- Construction: Calculating dimensions and material quantities frequently involves fractions.
- Science: Experiments often require precise measurements and ratios represented as fractions.
- Finance: Calculating interest rates, dividends, and portions of investments often involves fractions.
Trends and Latest Developments
Digital Tools and Apps
In today's digital age, several apps and online tools can help with fraction calculations. These tools are useful for both educational purposes and practical applications. Some examples include:
- Fraction Calculator Apps: These apps allow you to perform basic arithmetic operations on fractions, including addition, subtraction, multiplication, and division.
- Recipe Scaling Tools: Many websites and apps can automatically scale recipes up or down, calculating the new quantities of each ingredient, often involving fractions.
- Educational Websites: Websites like Khan Academy offer comprehensive lessons and practice exercises on fractions and mixed numbers.
Culinary Trends
Modern culinary trends often involve precise measurements and ratios, particularly in baking and pastry. Techniques like molecular gastronomy rely on understanding fractions and proportions to achieve specific textures and flavors. Additionally, the rise of home baking and cooking during recent years has increased the need for everyday individuals to understand and apply fractional math.
Data Analysis and Statistics
In data analysis, fractions and percentages are used extensively to represent proportions and ratios. Understanding how to manipulate and interpret these values is crucial for drawing meaningful conclusions from data. The ability to work with fractional data is a fundamental skill for anyone in fields such as market research, economics, and social sciences.
Expert Insights
According to culinary experts, accuracy in measurements is one of the most important factors in successful baking. Small variations in ingredient quantities can significantly affect the final product's texture, flavor, and appearance. Therefore, mastering the ability to calculate fractions and mixed numbers is essential for consistent results.
Financial analysts emphasize the importance of understanding fractional values when dealing with investments and financial instruments. The ability to calculate proportional returns and manage risk effectively often relies on a solid grasp of fractional math.
Tips and Expert Advice
Convert to Improper Fractions First
When dealing with mixed numbers, always convert them to improper fractions before performing any calculations. This simplifies the process and reduces the chance of errors.
For example, if you need to find 1/3 of 2 and 1/4 cups, first convert 2 and 1/4 to an improper fraction. 2 and 1/4 = (2 * 4 + 1) / 4 = 9/4. Then, multiply 9/4 by 1/3 to get 9/12, which simplifies to 3/4. So, 1/3 of 2 and 1/4 cups is 3/4 cup.
Simplify Fractions Whenever Possible
Before and after performing calculations, simplify fractions to their lowest terms. This makes the numbers easier to work with and helps you understand the quantities more clearly.
For instance, if you end up with a fraction like 4/8, simplify it to 1/2 by dividing both the numerator and denominator by their greatest common divisor, which is 4 in this case. Simplifying fractions makes it easier to compare and combine different quantities.
Use Visual Aids
Visual aids can be incredibly helpful when working with fractions, especially for those who are new to the concept. Draw diagrams or use physical objects like measuring cups to visualize the fractions.
For example, if you are trying to understand what 3/4 of a cup looks like, fill a measuring cup to the 3/4 mark. This provides a tangible representation of the fraction, making it easier to grasp the concept.
Practice Regularly
Like any mathematical skill, proficiency in working with fractions comes with practice. Solve a variety of problems involving fractions and mixed numbers to reinforce your understanding.
You can find practice problems in textbooks, online resources, and even in everyday situations like cooking or shopping. The more you practice, the more comfortable and confident you will become with fractions.
Double-Check Your Work
Always double-check your calculations to ensure accuracy. Fractions can be tricky, and it's easy to make a mistake, especially when dealing with mixed numbers and improper fractions.
Use a calculator or online tool to verify your answers. Additionally, ask a friend or family member to check your work. Catching errors early can save you time and frustration in the long run.
FAQ
Q: What is an improper fraction? An improper fraction is a fraction where the numerator (top number) is greater than or equal to the denominator (bottom number). For example, 5/4 is an improper fraction.
Q: How do I convert a mixed number to an improper fraction? Multiply the whole number by the denominator of the fraction, add the result to the numerator, and place the sum over the original denominator. For example, 2 and 1/3 = (2 * 3 + 1) / 3 = 7/3.
Q: How do I find half of a fraction? Multiply the fraction by 1/2. For example, half of 3/4 is (3/4) * (1/2) = 3/8.
Q: Why is it important to simplify fractions? Simplifying fractions makes them easier to understand and work with. It also allows you to compare and combine different fractions more easily.
Q: Can I use a calculator to solve fraction problems? Yes, calculators can be helpful for solving fraction problems, especially for complex calculations. However, it's important to understand the underlying concepts so that you can interpret the results correctly.
Conclusion
Calculating half of 1 and 3/4 cups is a straightforward process once you understand the fundamentals of fractions and mixed numbers. By converting the mixed number to an improper fraction and then multiplying by 1/2, you can easily find the desired quantity. This skill is invaluable in various real-world applications, from cooking and baking to construction and finance.
Now that you have a solid understanding of how to find half of 1 and 3/4 cups (or any mixed number, for that matter), it's time to put your knowledge into practice. Try scaling down your favorite recipes, calculating proportions for DIY projects, or even helping a friend with their math homework. Don't hesitate to use the tips and tools discussed in this article to make the process easier and more efficient. And remember, consistent practice is key to mastering this essential skill. So, go ahead, grab your measuring cups, and start calculating with confidence!
Latest Posts
Latest Posts
-
What Does High Specific Gravity Mean
Nov 18, 2025
-
Key Figures Of The Harlem Renaissance
Nov 18, 2025
-
Ways To Get Better At Math
Nov 18, 2025
-
Definition Of A Minor Arc Of A Circle
Nov 18, 2025
-
What Does The Range In Math Mean
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 And 3/4 Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.