Divide 100 By 1 2 And Add 100
sonusaeterna
Nov 21, 2025 · 11 min read
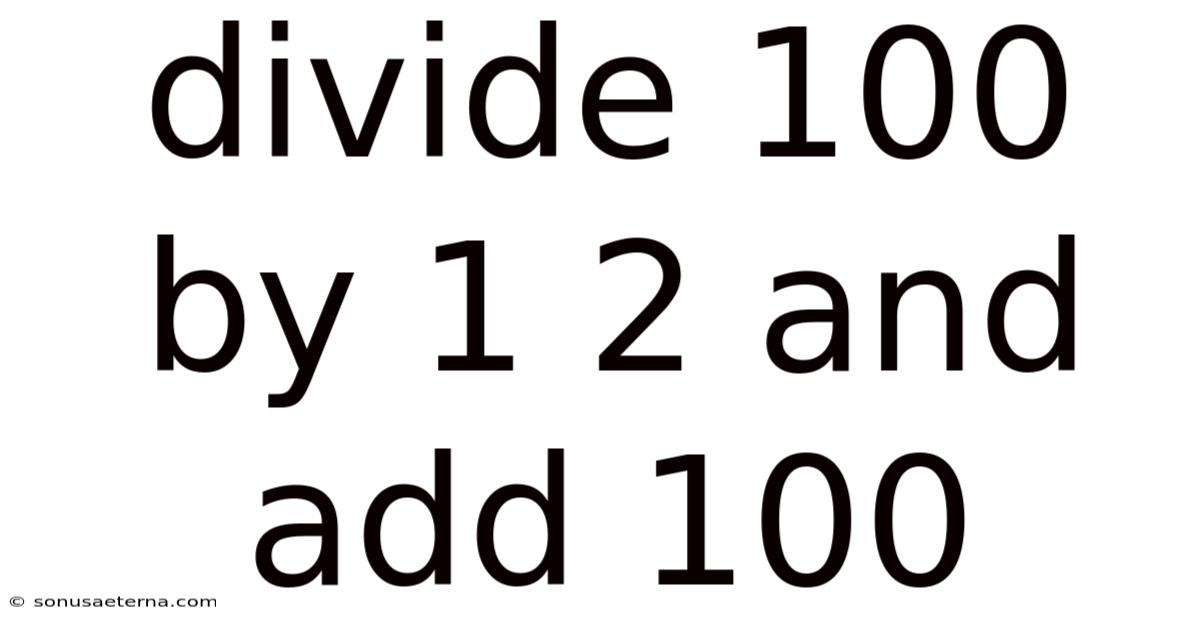
Table of Contents
Imagine you're at a lively math competition, and the final question flashes on the screen: "Divide 100 by 1/2 and add 100. What's the answer?" A wave of nervous excitement fills the room as contestants scribble away, some confidently nodding, others furrowing their brows in deep thought. It seems straightforward, but there's a subtle twist that can easily trip you up.
This seemingly simple math problem, "divide 100 by 1/2 and add 100," often leads to surprising answers. Many people quickly calculate 100 divided by 2 and then add 100, arriving at 150. However, the key lies in the correct interpretation of "divide 100 by 1/2." This article will explore the intricacies of this mathematical puzzle, offering a comprehensive explanation, examining its underlying principles, discussing common mistakes, and providing practical tips for solving it correctly. Whether you're a student, a math enthusiast, or simply curious, understanding this problem will sharpen your mathematical intuition and problem-solving skills.
Understanding the Basics of Dividing by Fractions
What Does "Divide 100 by 1/2" Really Mean?
The phrase "divide 100 by 1/2" is mathematically represented as 100 ÷ (1/2). This operation asks how many halves are in 100. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/2 is 2/1, which simplifies to 2. Therefore, dividing 100 by 1/2 is the same as multiplying 100 by 2. This fundamental concept is crucial for accurately solving the problem.
The Reciprocal Rule in Division
The reciprocal rule states that dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction a/b is b/a. This rule stems from the properties of multiplication and division, ensuring that the operation undoes the original fraction. For example, to divide 5 by 1/3, you multiply 5 by 3/1, which equals 15. This principle applies universally to all division involving fractions.
Why Does Dividing by a Fraction Work This Way?
The logic behind dividing by a fraction can be understood by considering what division represents. Division is essentially the inverse operation of multiplication. When you divide 100 by 1/2, you are asking, "How many halves fit into 100?" Since each whole number contains two halves, 100 whole numbers will contain 200 halves. Mathematically, this is equivalent to multiplying 100 by 2. Understanding this underlying concept makes it easier to remember and apply the reciprocal rule correctly.
Real-World Examples of Dividing by Fractions
Dividing by fractions is not just an abstract mathematical concept; it has practical applications in everyday life. Consider the following examples:
- Cooking: If a recipe calls for 1/4 cup of sugar per serving and you want to make 8 servings, you need to divide the total amount of sugar (which would be calculated if you knew how much sugar you had on hand) by 1/4. This is the same as multiplying by 4.
- Construction: If you need to cut a 10-foot plank into pieces that are 1/3 foot long, you would divide 10 by 1/3. This tells you how many pieces you can cut, which is 30.
- Travel: If you are traveling 150 miles and you cover 1/20 of the distance every 10 minutes, you can calculate how many 10-minute intervals it will take to complete the journey by dividing the total distance by 1/20.
Common Mistakes When Dividing by Fractions
Several common mistakes can occur when dividing by fractions, leading to incorrect answers:
- Forgetting to use the reciprocal: One of the most frequent errors is simply dividing the number by the denominator of the fraction without inverting the fraction.
- Misunderstanding the operation: Some people may confuse dividing by a fraction with multiplying by a fraction, leading to incorrect results.
- Incorrectly applying the order of operations: In more complex expressions, failing to adhere to the correct order of operations (PEMDAS/BODMAS) can result in errors.
Step-by-Step Solution: Divide 100 by 1/2 and Add 100
Breaking Down the Problem
To solve "divide 100 by 1/2 and add 100," we must follow the order of operations, which dictates that division should be performed before addition. The problem can be broken down into two steps:
- Divide 100 by 1/2.
- Add the result to 100.
Step 1: Divide 100 by 1/2
To divide 100 by 1/2, we use the reciprocal rule:
100 ÷ (1/2) = 100 * 2 = 200
So, 100 divided by 1/2 equals 200.
Step 2: Add 100 to the Result
Now that we have the result of the division (200), we add 100 to it:
200 + 100 = 300
Therefore, the final answer is 300.
Why the Order of Operations Matters
The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), is crucial for ensuring consistency in mathematical calculations. Without a standard order, the same expression could yield different results based on the order in which operations are performed. In this case, if we were to add 100 to 1 before dividing by 1/2, the result would be incorrect.
Common Pitfalls to Avoid
When solving this problem, there are several pitfalls to watch out for:
- Incorrectly interpreting the problem: Many people instinctively divide 100 by 2 instead of 1/2.
- Ignoring the order of operations: Adding before dividing will lead to a wrong answer.
- Not understanding the reciprocal: Failing to recognize that dividing by 1/2 is the same as multiplying by 2.
The Psychological Aspect of Solving Math Problems
Why Simple Math Problems Can Be Tricky
Simple math problems like "divide 100 by 1/2 and add 100" can be tricky because they often play on our intuitive, but sometimes flawed, understanding of numbers and operations. Our brains are wired to seek quick solutions, which can lead to overlooking crucial details or misinterpreting the problem's structure. This is particularly true under pressure, such as in a test environment or competition.
The Role of Cognitive Biases
Cognitive biases, which are systematic patterns of deviation from norm or rationality in judgment, can significantly impact our ability to solve math problems accurately. One common bias is the availability heuristic, where we rely on easily recalled information to make judgments. In this case, the simplicity of the numbers might lead us to quickly jump to an incorrect conclusion without fully analyzing the problem.
How to Overcome Mental Blocks
To overcome mental blocks and solve math problems more effectively, consider the following strategies:
- Read the problem carefully: Take your time to fully understand what the problem is asking before attempting to solve it.
- Break the problem down: Divide complex problems into smaller, more manageable steps.
- Use visual aids: Drawing diagrams or visualizing the problem can help clarify the relationships between numbers and operations.
- Check your work: Always review your calculations to catch any errors.
- Practice regularly: Consistent practice builds familiarity and confidence, reducing the likelihood of making mistakes.
The Importance of Mathematical Intuition
Mathematical intuition is the ability to understand mathematical concepts and relationships without consciously reasoning through each step. It's developed through practice and exposure to a wide range of problems. Cultivating mathematical intuition can help you quickly identify patterns, make educated guesses, and solve problems more efficiently.
Advanced Applications and Related Concepts
Extending the Concept to More Complex Fractions
The principle of dividing by fractions can be extended to more complex fractions and mixed numbers. For example, dividing 150 by 2 1/2 involves converting the mixed number to an improper fraction (5/2) and then multiplying 150 by the reciprocal (2/5). This process remains consistent regardless of the complexity of the fractions involved.
Division with Decimals and Percentages
Division with decimals and percentages is closely related to division with fractions. Decimals can be converted to fractions, and percentages can be expressed as decimals or fractions. For example, dividing by 0.25 is the same as dividing by 1/4, which is the same as multiplying by 4. Understanding these conversions makes it easier to solve a wide variety of mathematical problems.
Applications in Algebra and Calculus
The concept of dividing by fractions is fundamental in algebra and calculus. In algebra, it is used to simplify expressions and solve equations involving fractions. In calculus, it appears in various contexts, such as finding derivatives and integrals of rational functions. A solid understanding of dividing by fractions is essential for success in these higher-level math courses.
Exploring Number Theory
Number theory, a branch of mathematics that deals with the properties and relationships of numbers, also relies on the principles of division. Concepts such as divisibility, prime numbers, and modular arithmetic all involve division and its related operations. Understanding how to divide by fractions contributes to a broader understanding of number theory.
The Role of Division in Computer Science
Division is a fundamental operation in computer science. It is used in various algorithms and data structures, such as sorting, searching, and hashing. Understanding how division works, including division with fractions, is crucial for developing efficient and accurate computer programs.
Tips for Teaching and Learning Division
Strategies for Teachers
For teachers, effectively teaching division involves several key strategies:
- Use visual aids: Diagrams, manipulatives, and real-world examples can help students visualize the concept of division.
- Start with basic concepts: Ensure students have a solid understanding of basic division before introducing fractions.
- Emphasize the reciprocal rule: Clearly explain and demonstrate the reciprocal rule for dividing by fractions.
- Provide ample practice: Offer a variety of practice problems to reinforce learning.
- Address common mistakes: Identify and correct common mistakes to prevent misconceptions from solidifying.
Tips for Students
For students, improving their understanding of division involves:
- Review the basics: Ensure you have a strong foundation in basic arithmetic operations.
- Practice regularly: Consistent practice is key to mastering division.
- Seek help when needed: Don't hesitate to ask your teacher or classmates for help if you're struggling.
- Use online resources: There are many online resources available, such as videos, tutorials, and practice quizzes, that can help you improve your skills.
- Apply division to real-world problems: Look for opportunities to apply division in everyday situations to make learning more meaningful.
Making Math Fun
Making math fun can significantly enhance learning and engagement. Consider incorporating games, puzzles, and interactive activities into your study routine. These activities can help you develop a deeper understanding of mathematical concepts while also making learning more enjoyable.
Understanding Different Teaching Methodologies
Different teaching methodologies can impact how students learn division. Some methodologies emphasize rote memorization, while others focus on conceptual understanding. It's important to find a teaching method that aligns with your learning style and helps you develop a strong foundation in division.
FAQ: Divide 100 by 1/2 and Add 100
Q: What is the correct way to solve "divide 100 by 1/2 and add 100"?
A: First, divide 100 by 1/2, which equals 200. Then, add 100 to 200, resulting in 300.
Q: Why do we multiply by the reciprocal when dividing by a fraction?
A: Multiplying by the reciprocal is equivalent to asking how many of the fraction fit into the number. It's the inverse operation of multiplication and ensures accurate division.
Q: What is the order of operations?
A: The order of operations is PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction).
Q: What are common mistakes when solving this problem?
A: Common mistakes include dividing 100 by 2 instead of 1/2, ignoring the order of operations, and not understanding the reciprocal rule.
Q: How can I improve my division skills?
A: Practice regularly, review the basics, seek help when needed, and use online resources.
Conclusion
The seemingly straightforward math problem, "divide 100 by 1/2 and add 100," highlights the importance of understanding fundamental mathematical principles and the correct order of operations. By accurately interpreting the problem, applying the reciprocal rule, and avoiding common pitfalls, we arrive at the correct answer: 300. This exercise not only sharpens our mathematical skills but also illustrates how easily our intuition can mislead us if we're not careful.
Now that you've mastered this tricky problem, challenge yourself with similar mathematical puzzles. Share this article with your friends and family to test their math skills and spark engaging discussions. And remember, continuous practice and a solid understanding of basic concepts are key to excelling in mathematics. What other math riddles can you solve?
Latest Posts
Latest Posts
-
Outline The Levels Of Organization Starting With The Smallest Organisms
Nov 21, 2025
-
How Many Cubic Liters In A Cubic Foot
Nov 21, 2025
-
Can You Stop Being A Jackass Meme
Nov 21, 2025
-
What Is The Molar Mass Of Nh4 2so4
Nov 21, 2025
-
What Are The New Testament Books
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about Divide 100 By 1 2 And Add 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.