Cos X/1-sin X + Cos X/1+sin X
sonusaeterna
Nov 20, 2025 · 18 min read
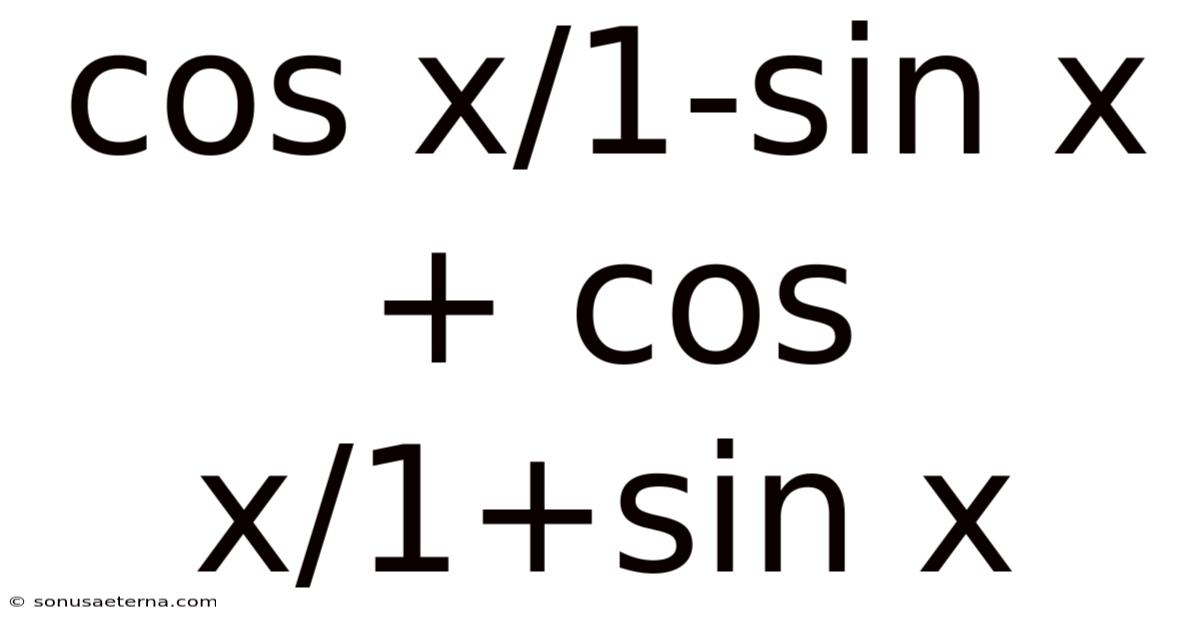
Table of Contents
Have you ever stumbled upon a mathematical expression that looks intimidating at first glance but simplifies beautifully with the right approach? Trigonometric expressions can often feel this way, especially when they involve fractions and different trigonometric functions. Expressions like cos x/1-sin x + cos x/1+sin x might seem complex, but they offer a fascinating glimpse into the elegance and interconnectedness of trigonometric identities. Understanding how to simplify these expressions not only enhances your mathematical skills but also deepens your appreciation for the inherent beauty and order within mathematics.
Simplifying trigonometric expressions is more than just an academic exercise; it's a practical skill that finds applications in various fields, from physics and engineering to computer graphics and data analysis. Whether you're modeling waveforms, designing structures, or developing algorithms, the ability to manipulate trigonometric functions efficiently can significantly streamline your work. This exploration will guide you through the simplification of the expression cos x/1-sin x + cos x/1+sin x, revealing the underlying principles and demonstrating the power of strategic mathematical manipulation.
Unveiling the Trigonometric Expression: cos x/1-sin x + cos x/1+sin x
The expression cos x/1-sin x + cos x/1+sin x is a classic example of a trigonometric problem that, despite its initial complexity, can be simplified to a much more manageable form. Trigonometric expressions often involve various functions like sine, cosine, tangent, and their reciprocals, combined through arithmetic operations. Simplifying such expressions involves applying trigonometric identities and algebraic manipulations to reduce them to their simplest form, making them easier to understand and use in further calculations.
At its core, trigonometry deals with the relationships between the angles and sides of triangles, particularly right triangles. These relationships are encapsulated in trigonometric functions, which relate an angle to ratios of sides. The expression cos x/1-sin x + cos x/1+sin x involves two fundamental trigonometric functions: cosine (cos x) and sine (sin x). To simplify this expression, we need to understand the properties of these functions and how they interact with each other.
Essential Trigonometric Concepts
Before diving into the simplification process, let’s revisit some essential trigonometric concepts:
-
Sine (sin x): In a right triangle, the sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse.
-
Cosine (cos x): The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
-
Pythagorean Identity: One of the most fundamental trigonometric identities is sin²x + cos²x = 1, which is derived from the Pythagorean theorem. This identity is crucial for simplifying many trigonometric expressions.
-
Reciprocal Identities: These include identities like csc x = 1/sin x, sec x = 1/cos x, and cot x = 1/tan x.
-
Quotient Identities: These relate tangent and cotangent to sine and cosine, such as tan x = sin x/cos x and cot x = cos x/sin x.
Historical Roots of Trigonometry
Trigonometry has ancient roots, with early developments in ancient Egypt, Mesopotamia, and Greece. The study of angles and their relationships to sides of triangles was initially driven by practical needs such as navigation, surveying, and astronomy.
Ancient Egypt and Mesopotamia: Early Egyptians and Babylonians used trigonometry in rudimentary forms for land surveying and constructing pyramids. The Babylonian sexagesimal (base-60) number system influenced the division of a circle into 360 degrees.
Ancient Greece: Greek mathematicians made significant contributions to trigonometry. Hipparchus of Nicaea (c. 190-120 BC) is often credited as the "father of trigonometry" for his systematic study of trigonometric functions. Ptolemy (c. 90-168 AD) further developed trigonometry in his book Almagest, which included detailed tables of chords (related to sines) and astronomical observations.
Indian Mathematics: Indian mathematicians like Aryabhata (476-550 AD) and Brahmagupta (598-668 AD) made substantial contributions by introducing the sine function and developing trigonometric tables. Their work was later transmitted to the Islamic world and eventually to Europe.
Islamic World: Islamic scholars translated and expanded upon Greek and Indian mathematical texts. They refined trigonometric methods and created accurate trigonometric tables, which were crucial for astronomical calculations.
European Renaissance: During the Renaissance, European mathematicians rediscovered and built upon the trigonometric knowledge of the Greeks, Indians, and Islamic scholars. Trigonometry became an essential tool in navigation, astronomy, and the development of calculus.
Why Simplify Trigonometric Expressions?
Simplifying trigonometric expressions serves several important purposes:
- Ease of Calculation: Simplified expressions are easier to evaluate and manipulate in further calculations.
- Clarity: Simplification reveals the underlying structure of the expression, making it easier to understand.
- Problem Solving: Simplified forms can make it easier to solve equations and prove identities.
- Applications: In various fields, simplified trigonometric expressions can streamline modeling and analysis.
Understanding these essential concepts and historical context sets the stage for a detailed exploration of how to simplify the expression cos x/1-sin x + cos x/1+sin x. The next sections will guide you through the step-by-step process, highlighting the key techniques and identities used in simplification.
Comprehensive Overview: Simplifying cos x/1-sin x + cos x/1+sin x
To simplify the expression cos x/1-sin x + cos x/1+sin x, we will combine the two fractions into a single fraction, simplify the numerator using trigonometric identities, and then reduce the expression to its simplest form. Here’s a step-by-step breakdown:
Step 1: Combine the Fractions
The first step is to combine the two fractions by finding a common denominator. The common denominator for (1 - sin x) and (1 + sin x) is their product, which is (1 - sin x)(1 + sin x).
So, we rewrite the expression as:
cos x/(1 - sin x) + cos x/(1 + sin x) = [cos x(1 + sin x) + cos x(1 - sin x)] / [(1 - sin x)(1 + sin x)]
Step 2: Expand the Numerator
Next, we expand the numerator by distributing cos x across both terms in each parenthesis:
cos x(1 + sin x) + cos x(1 - sin x) = cos x + cos x sin x + cos x - cos x sin x
Step 3: Simplify the Numerator
Now, we simplify the numerator by combining like terms:
cos x + cos x sin x + cos x - cos x sin x = 2 cos x
Notice that the terms cos x sin x and -cos x sin x cancel each other out, leaving us with 2 cos x.
Step 4: Expand the Denominator
Expand the denominator using the difference of squares formula, which states that (a - b)(a + b) = a² - b²:
(1 - sin x)(1 + sin x) = 1² - (sin x)² = 1 - sin²x
Step 5: Apply the Pythagorean Identity
Recall the Pythagorean identity: sin²x + cos²x = 1. We can rearrange this identity to express cos²x in terms of sin²x:
cos²x = 1 - sin²x
Now, substitute this into the denominator:
1 - sin²x = cos²x
Step 6: Simplify the Entire Expression
Now, we have the simplified numerator and denominator:
Numerator: 2 cos x
Denominator: cos²x
So, the entire expression becomes:
(2 cos x) / (cos²x)
We can further simplify this by canceling out a factor of cos x from the numerator and denominator:
(2 cos x) / (cos²x) = 2 / cos x
Step 7: Use Reciprocal Identity
Finally, recall the reciprocal identity: sec x = 1 / cos x. Therefore, we can rewrite the expression as:
2 / cos x = 2 sec x
Thus, the simplified form of the expression cos x/1-sin x + cos x/1+sin x is 2 sec x.
Alternative Methods and Insights
While the above method is straightforward, there are alternative approaches to simplifying the expression, which can provide additional insights.
Method 2: Using Conjugate Multiplication
Another approach involves multiplying the numerator and denominator of each fraction by the conjugate of the denominator. The conjugate of (1 - sin x) is (1 + sin x), and the conjugate of (1 + sin x) is (1 - sin x).
-
Multiply the first fraction by (1 + sin x) / (1 + sin x):
cos x / (1 - sin x) * (1 + sin x) / (1 + sin x) = (cos x (1 + sin x)) / (1 - sin²x) = (cos x (1 + sin x)) / cos²x = (1 + sin x) / cos x
-
Multiply the second fraction by (1 - sin x) / (1 - sin x):
cos x / (1 + sin x) * (1 - sin x) / (1 - sin x) = (cos x (1 - sin x)) / (1 - sin²x) = (cos x (1 - sin x)) / cos²x = (1 - sin x) / cos x
-
Add the Simplified Fractions:
Now add the two simplified fractions:
(1 + sin x) / cos x + (1 - sin x) / cos x = (1 + sin x + 1 - sin x) / cos x = 2 / cos x
-
Use Reciprocal Identity:
As before, use the reciprocal identity sec x = 1 / cos x:
2 / cos x = 2 sec x
This method yields the same result, 2 sec x, and demonstrates the versatility of trigonometric simplification techniques.
The Significance of Understanding Trigonometric Identities
The simplification of cos x/1-sin x + cos x/1+sin x highlights the importance of mastering trigonometric identities. These identities act as tools that allow us to transform complex expressions into simpler, more manageable forms. Without a solid understanding of identities like the Pythagorean identity and reciprocal identities, simplifying such expressions would be considerably more challenging.
Furthermore, this exercise underscores the value of algebraic manipulation skills. Combining fractions, expanding terms, and canceling out common factors are fundamental algebraic techniques that are essential for simplifying trigonometric expressions. The ability to apply these skills effectively is crucial for success in trigonometry and related fields.
In conclusion, simplifying the expression cos x/1-sin x + cos x/1+sin x not only provides a concrete example of trigonometric simplification but also reinforces the importance of understanding trigonometric identities and algebraic techniques. The result, 2 sec x, is a testament to the power of strategic mathematical manipulation.
Trends and Latest Developments in Trigonometry
Trigonometry, while rooted in ancient mathematics, continues to evolve with modern applications and computational advancements. Current trends focus on leveraging trigonometric principles in digital technologies, data analysis, and interdisciplinary fields.
Computational Trigonometry
With the rise of powerful computing, computational trigonometry has become increasingly important. This field involves developing efficient algorithms for computing trigonometric functions and solving trigonometric equations. These algorithms are crucial in computer graphics, simulations, and data processing.
Fast Fourier Transform (FFT): The FFT is a prime example of computational trigonometry in action. It uses trigonometric functions to decompose complex signals into simpler components, enabling efficient signal processing and data analysis.
Numerical Methods: Numerical methods like Newton-Raphson and iterative techniques are employed to solve complex trigonometric equations that lack analytical solutions. These methods are essential in engineering and scientific computations.
Trigonometry in Machine Learning
Trigonometric functions and concepts are finding applications in machine learning, particularly in areas like neural networks and data analysis.
Activation Functions: Trigonometric functions like sine and cosine are used as activation functions in neural networks. These functions introduce non-linearity, allowing neural networks to model complex relationships in data.
Time Series Analysis: Trigonometry is used to analyze and predict patterns in time series data. Techniques like Fourier analysis decompose time series into trigonometric components, revealing underlying trends and periodicities.
Interdisciplinary Applications
Trigonometry's versatility extends into various interdisciplinary fields, where it provides valuable tools for modeling and analyzing complex phenomena.
Medical Imaging: Trigonometric principles are used in medical imaging techniques like CT scans and MRI. These techniques use trigonometric transformations to reconstruct images of the human body from data collected by sensors.
Geospatial Analysis: Trigonometry is fundamental to geospatial analysis, which involves analyzing geographic data. Techniques like triangulation and coordinate transformations rely on trigonometric functions to map and analyze spatial relationships.
Latest Data and Research
Recent research highlights the ongoing relevance of trigonometry in both theoretical and applied contexts.
Advanced Materials: Researchers are using trigonometric models to design and analyze advanced materials with specific properties. For example, trigonometric functions can describe the arrangement of atoms in crystal lattices, aiding in the development of new materials with desired mechanical or electrical properties.
Quantum Computing: Trigonometric functions play a crucial role in quantum mechanics, which is the foundation of quantum computing. Quantum algorithms rely on trigonometric transformations to manipulate quantum states and perform computations.
Professional Insights
As technology advances, the role of trigonometry in various fields is expected to grow. Professionals in fields like engineering, computer science, and data science need a strong foundation in trigonometry to tackle complex problems and develop innovative solutions.
Continuing Education: Professionals should stay updated with the latest developments in computational trigonometry and its applications in their respective fields. Online courses, workshops, and conferences provide opportunities to learn new techniques and tools.
Interdisciplinary Collaboration: Collaboration between mathematicians, engineers, and scientists is essential for advancing the applications of trigonometry. By working together, they can develop new models, algorithms, and technologies that leverage the power of trigonometry.
In summary, trigonometry continues to be a vibrant and evolving field with applications ranging from computational algorithms to interdisciplinary research. Staying abreast of these trends and developments is crucial for professionals seeking to leverage trigonometry in their work.
Tips and Expert Advice for Mastering Trigonometric Simplification
Mastering trigonometric simplification requires a combination of theoretical knowledge and practical application. Here are some tips and expert advice to help you enhance your skills:
1. Master the Fundamental Identities
The cornerstone of trigonometric simplification is a thorough understanding of fundamental identities. These include:
- Pythagorean Identities: sin²x + cos²x = 1, 1 + tan²x = sec²x, 1 + cot²x = csc²x
- Reciprocal Identities: csc x = 1/sin x, sec x = 1/cos x, cot x = 1/tan x
- Quotient Identities: tan x = sin x/cos x, cot x = cos x/sin x
- Angle Sum and Difference Identities: sin(a ± b), cos(a ± b), tan(a ± b)
- Double Angle Identities: sin(2x), cos(2x), tan(2x)
- Half Angle Identities: sin(x/2), cos(x/2), tan(x/2)
Make flashcards, practice problems, and regularly review these identities to ensure they become second nature. The more familiar you are with these identities, the easier it will be to recognize opportunities for simplification.
2. Practice Regularly
Like any mathematical skill, proficiency in trigonometric simplification comes with practice. Work through a variety of problems, starting with simpler ones and gradually progressing to more complex examples.
Start with Basic Simplifications: Begin by simplifying expressions that involve only one or two identities. For example, simplify expressions involving sin²x + cos²x or converting between tan x and sin x/cos x.
Progress to Complex Problems: Once you are comfortable with basic simplifications, tackle more challenging problems that require multiple steps and the application of several identities. The more you practice, the better you will become at recognizing patterns and choosing the right strategies.
3. Develop Algebraic Proficiency
Trigonometric simplification often involves algebraic manipulation. Brush up on your algebraic skills, including:
- Factoring: Learn to factor expressions involving trigonometric functions, such as factoring out a common factor or using the difference of squares formula.
- Combining Fractions: Practice adding, subtracting, multiplying, and dividing fractions that contain trigonometric functions.
- Rationalizing Denominators: Be able to rationalize denominators by multiplying by a conjugate, especially when dealing with expressions involving square roots.
Strong algebraic skills will allow you to manipulate trigonometric expressions more effectively and efficiently.
4. Look for Patterns and Strategic Substitutions
Effective trigonometric simplification involves recognizing patterns and making strategic substitutions.
Identify Opportunities for Simplification: As you work through problems, look for opportunities to apply trigonometric identities. For example, if you see sin²x, consider whether you can use the Pythagorean identity to replace it with 1 - cos²x.
Make Strategic Substitutions: When you identify a potential simplification, make the substitution and see if it leads to further simplification. Sometimes, you may need to try different substitutions before finding the most effective approach.
5. Use Conjugate Multiplication
Conjugate multiplication can be a powerful technique for simplifying trigonometric expressions, especially those involving fractions.
Multiply by the Conjugate: If you have an expression with a denominator of the form a + b, multiply both the numerator and denominator by the conjugate a - b. This will often eliminate square roots or simplify the expression.
Recognize When to Use Conjugates: Practice recognizing situations where conjugate multiplication is likely to be helpful. This technique is particularly useful when dealing with expressions involving 1 ± sin x or 1 ± cos x.
6. Check Your Work
Always check your work to ensure that you have simplified the expression correctly.
Substitute Values: Choose a few values for the variable (e.g., x = 0, π/4, π/2) and evaluate both the original expression and the simplified expression. If the values are the same, you have likely simplified the expression correctly.
Use a Computer Algebra System (CAS): Tools like Mathematica, Maple, or Wolfram Alpha can be used to check your work. Enter the original expression and the simplified expression, and see if the CAS confirms that they are equivalent.
7. Understand the Unit Circle
The unit circle is a visual representation of trigonometric functions that can aid in understanding and simplification.
Visualize Trigonometric Values: Use the unit circle to visualize the values of sine, cosine, tangent, and other trigonometric functions for different angles. This can help you gain a better understanding of how these functions behave and how they relate to each other.
Identify Relationships: The unit circle can also help you identify relationships between trigonometric functions, such as the fact that sin(x) = cos(π/2 - x) and cos(x) = sin(π/2 - x).
8. Seek Help and Collaboration
Don't hesitate to seek help from teachers, tutors, or classmates if you are struggling with trigonometric simplification.
Ask Questions: If you are unsure about a particular step or concept, ask questions. Understanding the underlying principles is crucial for mastering trigonometric simplification.
Collaborate with Others: Work with classmates or form study groups to discuss problems and share strategies. Collaborating with others can provide new insights and perspectives that you may not have considered on your own.
By following these tips and expert advice, you can enhance your skills in trigonometric simplification and gain a deeper understanding of trigonometry.
FAQ: Simplifying Trigonometric Expressions
Here are some frequently asked questions about simplifying trigonometric expressions:
Q: Why is it important to simplify trigonometric expressions?
A: Simplifying trigonometric expressions makes them easier to understand, evaluate, and use in further calculations. Simplified expressions reveal the underlying structure, which can aid in problem-solving and applications in various fields like physics, engineering, and computer science.
Q: What is the most common mistake when simplifying trigonometric expressions?
A: One of the most common mistakes is incorrectly applying trigonometric identities. It's crucial to ensure that the identity is used in the correct context and that the algebraic manipulations are accurate. Another common mistake is overlooking opportunities to factor or combine terms.
Q: How can I remember all the trigonometric identities?
A: While memorization is helpful, understanding the derivations of the identities can make them easier to remember. Focus on the fundamental identities (like the Pythagorean identity) and understand how other identities are derived from them. Regular practice and using flashcards can also aid in memorization.
Q: When should I use conjugate multiplication in simplifying trigonometric expressions?
A: Conjugate multiplication is particularly useful when dealing with fractions that have denominators of the form a + b or a - b, where a and b involve trigonometric functions (e.g., 1 + sin x or 1 - cos x). Multiplying the numerator and denominator by the conjugate can help eliminate square roots or simplify the expression.
Q: Can I use a calculator to simplify trigonometric expressions?
A: While calculators can help evaluate trigonometric functions, they are not typically used for simplifying expressions. Simplifying expressions requires algebraic manipulation and the application of trigonometric identities, which is best done manually. However, calculators and computer algebra systems can be used to check your work.
Q: What is the Pythagorean identity, and why is it so important?
A: The Pythagorean identity is sin²x + cos²x = 1. It is derived from the Pythagorean theorem and is one of the most fundamental trigonometric identities. It's essential because it relates sine and cosine, allowing you to express one in terms of the other, which is crucial for simplifying many trigonometric expressions.
Q: How do I know if I have simplified an expression completely?
A: An expression is typically considered simplified if it contains the fewest possible terms and trigonometric functions. A simplified expression should also be easier to evaluate and manipulate. If you're unsure, try checking your work by substituting values or using a computer algebra system to verify that your simplified expression is equivalent to the original.
Q: Are there any online resources that can help me practice simplifying trigonometric expressions?
A: Yes, there are many online resources available, including websites like Khan Academy, Wolfram Alpha, and various educational platforms. These resources offer practice problems, tutorials, and step-by-step solutions to help you improve your skills.
Conclusion
In summary, the journey through simplifying cos x/1-sin x + cos x/1+sin x illustrates the elegance and power of trigonometric identities and algebraic manipulation. By combining fractions, applying the Pythagorean identity, and using reciprocal identities, we transformed a complex expression into a simple, elegant form: 2 sec x. This exercise not only enhances mathematical skills but also underscores the importance of strategic problem-solving and a deep understanding of fundamental trigonometric concepts.
Moreover, we explored the latest trends and developments in trigonometry, highlighting its continued relevance in computational mathematics, machine learning, and interdisciplinary applications. These insights reveal that trigonometry is not merely an academic subject but a vital tool for solving real-world problems and driving technological innovation.
To further your understanding and mastery of trigonometric simplification, we encourage you to practice regularly, master the fundamental identities, and seek help when needed. By doing so, you'll not only improve your mathematical skills but also gain a deeper appreciation for the beauty and interconnectedness of mathematics.
Ready to put your knowledge to the test? Try simplifying similar trigonometric expressions and share your solutions in the comments below! Let’s continue the journey of mathematical discovery together.
Latest Posts
Latest Posts
-
Do The Easter Island Heads Have Bodies
Nov 20, 2025
-
What Is An Act Of Supremacy
Nov 20, 2025
-
What Is The Color Of A Whale Shark
Nov 20, 2025
-
How Was Imperialism A Cause Of World War 1
Nov 20, 2025
-
What Is The Half Of 16
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about Cos X/1-sin X + Cos X/1+sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.