9 4 As A Mixed Number
sonusaeterna
Nov 15, 2025 · 13 min read
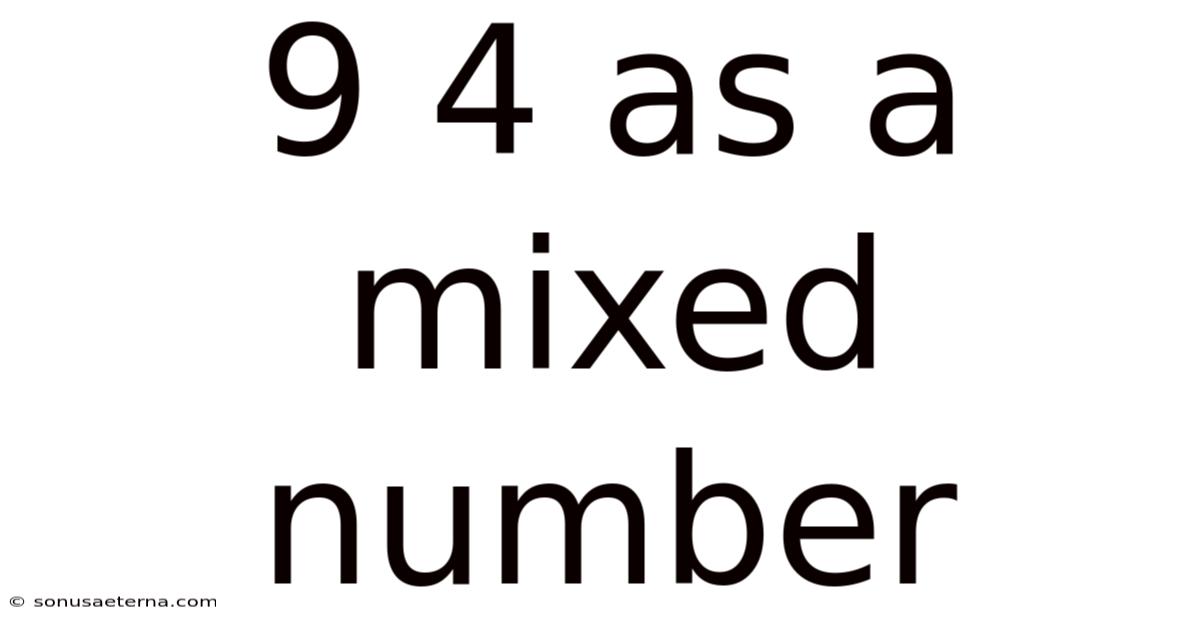
Table of Contents
Imagine you're baking a cake and the recipe calls for a specific amount of flour, say 9/4 cups. You grab your measuring cups, but realize they only measure in whole cups and fractions less than one. This is where understanding 9/4 as a mixed number becomes incredibly useful. It allows you to easily measure out the ingredients using your available tools, ensuring your cake turns out perfectly.
Understanding fractions can sometimes feel like navigating a maze. However, with a bit of guidance, even seemingly complex fractions like 9/4 can be easily deciphered. Converting an improper fraction like 9/4 into a mixed number isn't just a mathematical exercise; it's a practical skill that simplifies everyday tasks and provides a deeper understanding of numerical relationships. It allows us to express quantities in a more intuitive and manageable way.
Understanding Fractions and Mixed Numbers
Fractions are a fundamental part of mathematics, representing a portion of a whole. They consist of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we have.
In the case of 9/4, the denominator (4) tells us that the whole is divided into four equal parts, and the numerator (9) tells us that we have nine of those parts. This is an improper fraction because the numerator is larger than the denominator. An improper fraction represents a quantity greater than one whole.
A mixed number, on the other hand, combines a whole number and a proper fraction (where the numerator is smaller than the denominator). For example, 2 1/2 is a mixed number, representing two whole units and one-half of another unit.
The process of converting an improper fraction like 9/4 into a mixed number involves determining how many whole units are contained within the fraction and what fraction remains after extracting those whole units. This conversion simplifies the representation of the quantity, making it easier to visualize and understand.
Historically, fractions have played a crucial role in various fields, from ancient land surveying and trade to modern engineering and scientific research. The ability to manipulate and understand fractions is essential for solving practical problems and developing a strong foundation in mathematics. The concept of a mixed number emerged as a natural way to represent quantities that fall between whole numbers, providing a more intuitive and accessible way to express partial amounts.
The Mathematical Foundation of Converting Improper Fractions
The conversion from an improper fraction to a mixed number relies on the mathematical principles of division and remainders. When we divide the numerator by the denominator, the quotient (the result of the division) represents the whole number part of the mixed number, and the remainder represents the numerator of the fractional part. The denominator of the fractional part remains the same as the original denominator.
For instance, in the case of 9/4, we perform the division 9 ÷ 4. The quotient is 2, and the remainder is 1. This means that 9/4 contains two whole units (2) and a remainder of 1 part out of the 4 parts that make up a whole (1/4). Therefore, the mixed number equivalent of 9/4 is 2 1/4.
This process can be expressed mathematically as follows:
- Given an improper fraction a/b, where a > b:
- Divide a by b to obtain a quotient q and a remainder r.
- The mixed number is then q r/b.
The key is understanding that the improper fraction represents a quantity that can be broken down into whole units and a remaining fractional part. The division process allows us to separate these components and express the quantity in a more understandable format.
Visualizing the Conversion
Visual aids can significantly enhance understanding, especially when dealing with fractions. Imagine a pie cut into four equal slices (representing the denominator of 4). The fraction 9/4 represents having nine of these slices.
To visualize the conversion to a mixed number, you can group the slices into whole pies. Since each pie requires four slices, you can create two whole pies from eight of the nine slices. This leaves you with one remaining slice, which represents 1/4 of a pie.
Therefore, visually, 9/4 represents two whole pies and one-quarter of another pie, which corresponds to the mixed number 2 1/4. This visual representation reinforces the idea that an improper fraction can be expressed as a combination of whole units and a fractional part.
Another helpful visualization is using number lines. Mark intervals of 1/4 on a number line. You will see that 9/4 falls between 2 and 3. By counting the intervals, you can confirm that 9/4 is equivalent to 2 and 1/4. This method is especially useful for comparing different fractions and understanding their relative values.
Importance of Mixed Numbers
Mixed numbers are particularly useful in practical applications because they provide a more intuitive way to represent quantities. For example, if you are measuring fabric for a sewing project, you might need 2 1/2 meters. This is much easier to understand and measure than 5/2 meters.
Mixed numbers are also essential in various mathematical operations. While improper fractions are often preferred for calculations involving multiplication and division, mixed numbers are more convenient for addition and subtraction, especially when dealing with real-world problems.
Furthermore, understanding mixed numbers is crucial for developing a strong foundation in arithmetic and algebra. It helps students grasp the concept of fractions and their relationship to whole numbers, which is essential for more advanced mathematical topics. By mastering the conversion between improper fractions and mixed numbers, students can gain confidence in their ability to manipulate and understand numerical quantities.
Trends and Latest Developments
While the basic principles of converting improper fractions to mixed numbers remain unchanged, there are some trends and developments in how this concept is taught and applied.
One notable trend is the increased emphasis on visual and interactive learning tools. Educators are using online simulations, virtual manipulatives, and interactive whiteboards to help students visualize fractions and understand the conversion process. These tools can make learning more engaging and effective, particularly for students who struggle with abstract concepts.
Another trend is the integration of real-world applications into the curriculum. Instead of simply focusing on rote memorization of rules, educators are presenting students with practical problems that require them to use fractions and mixed numbers in meaningful ways. This approach helps students see the relevance of mathematics in their daily lives and motivates them to learn.
Furthermore, there is growing interest in using technology to automate the conversion process. Various online calculators and mobile apps can quickly convert improper fractions to mixed numbers, making it easier for students and professionals to perform calculations accurately. However, it is important to emphasize that these tools should be used to supplement, not replace, a fundamental understanding of the underlying mathematical principles.
From a professional standpoint, industries like construction, cooking, and manufacturing heavily rely on accurate fraction and mixed number conversions. Modern software and tools used in these fields often have built-in functionalities to handle these calculations efficiently. Professionals are expected to not only use these tools but also to understand the underlying math to ensure accuracy and troubleshoot any issues.
Expert Insights
Experts in mathematics education emphasize the importance of conceptual understanding over procedural fluency. While it is important for students to be able to convert improper fractions to mixed numbers accurately, it is even more important for them to understand why the process works and what the resulting mixed number represents.
According to Dr. Sarah Miller, a professor of mathematics education at the University of California, "Students should not just memorize the steps for converting an improper fraction to a mixed number. They need to understand the relationship between fractions and division, and how the quotient and remainder relate to the whole number and fractional parts of the mixed number."
Another expert, Mr. David Lee, a high school math teacher, suggests using real-world examples to illustrate the concept. "I often use cooking recipes or construction plans to show students how fractions and mixed numbers are used in practical situations. This helps them see the relevance of the math and makes it more engaging."
Moreover, experts recommend using a variety of teaching methods to cater to different learning styles. Some students may benefit from visual aids, while others may prefer hands-on activities or algebraic explanations. By using a combination of approaches, educators can ensure that all students have the opportunity to understand the concept fully.
Tips and Expert Advice
Converting 9/4 as a mixed number is a straightforward process once you understand the underlying concept. Here are some tips and expert advice to help you master this skill:
-
Understand the Meaning of Fractions: Make sure you have a solid grasp of what fractions represent. Remember that the denominator indicates the number of equal parts in a whole, and the numerator indicates the number of those parts you have.
- For example, if you're struggling with 9/4, think of it as nine quarters. If you have four quarters, you have one whole. This can help you visualize how many wholes are contained within the fraction.
-
Practice Division: The conversion process relies on division. Practice dividing the numerator by the denominator to find the quotient and remainder.
- Use long division if necessary to ensure you get the correct quotient and remainder. Accuracy in division is crucial for accurate conversion.
- There are online resources and apps that can help you practice division skills if you need to improve.
-
Visualize the Process: Use visual aids such as pie charts or number lines to help you understand the conversion process.
- Draw a pie chart and divide it into four equal slices. Shade nine of these slices and then group them into whole pies. This can help you see how many whole pies and leftover slices you have.
- Use a number line to plot the fraction 9/4 and then see how many whole numbers it contains and what fraction is left over.
-
Use Real-World Examples: Relate the concept to real-world situations that you encounter in your daily life.
- Think about dividing a pizza into slices or measuring ingredients for a recipe. These examples can help you see the practical applications of converting improper fractions to mixed numbers.
- For instance, imagine you have 9 cookies and you want to share them equally among 4 friends. Each friend gets 2 whole cookies and 1/4 of another cookie.
-
Check Your Work: After converting an improper fraction to a mixed number, check your work by converting the mixed number back to an improper fraction.
- To convert a mixed number back to an improper fraction, multiply the whole number by the denominator and then add the numerator. The result is the new numerator, and the denominator remains the same.
- For example, to convert 2 1/4 back to an improper fraction, multiply 2 by 4 to get 8, and then add 1 to get 9. The improper fraction is 9/4.
-
Use Online Resources: Take advantage of online calculators and educational websites to help you practice and learn.
- There are many websites and apps that can convert improper fractions to mixed numbers automatically. Use these tools to check your work and learn from your mistakes.
- Explore online tutorials and videos that explain the conversion process in a clear and concise manner.
-
Simplify When Possible: Always make sure to simplify the fractional part of the mixed number if possible.
- For example, if you end up with a mixed number like 2 2/4, you should simplify it to 2 1/2 because 2/4 can be simplified to 1/2. This makes the mixed number easier to understand and use.
-
Practice Regularly: Like any skill, converting improper fractions to mixed numbers requires practice. The more you practice, the more confident and proficient you will become.
- Set aside some time each day to practice converting different improper fractions to mixed numbers. Start with simple fractions and then gradually work your way up to more complex ones.
- Use flashcards or online quizzes to test your knowledge and track your progress.
By following these tips and practicing regularly, you can master the skill of converting improper fractions to mixed numbers and gain a deeper understanding of fractions in general.
FAQ
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). For example, 9/4 and 5/5 are improper fractions.
Q: What is a mixed number?
A: A mixed number is a combination of a whole number and a proper fraction (a fraction where the numerator is less than the denominator). For example, 2 1/4 is a mixed number.
Q: How do I convert an improper fraction to a mixed number?
A: To convert an improper fraction to a mixed number, divide the numerator by the denominator. The quotient (the result of the division) becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator remains the same.
Q: Why is it important to know how to convert improper fractions to mixed numbers?
A: Converting improper fractions to mixed numbers makes it easier to understand and visualize the quantity represented by the fraction. Mixed numbers are also more convenient for practical applications, such as measuring ingredients for a recipe or calculating lengths in a construction project.
Q: Can I use a calculator to convert improper fractions to mixed numbers?
A: Yes, there are many online calculators and mobile apps that can convert improper fractions to mixed numbers automatically. However, it is important to understand the underlying mathematical principles so that you can check your work and solve problems even without a calculator.
Q: What do I do if the fractional part of my mixed number can be simplified?
A: If the fractional part of your mixed number can be simplified, you should simplify it. For example, if you end up with 2 2/4, you should simplify it to 2 1/2.
Q: Is there an easier way to visualize converting 9/4 to a mixed number?
A: Think of 9/4 as having nine quarters. You know that four quarters make a dollar (one whole). So, eight quarters make two dollars (two wholes), and you have one quarter (1/4) left over. Therefore, 9/4 is the same as 2 1/4.
Conclusion
Understanding how to express 9/4 as a mixed number is a fundamental skill in mathematics with practical applications in everyday life. By dividing the numerator by the denominator, we find that 9/4 is equivalent to the mixed number 2 1/4. This means that 9/4 represents two whole units and one-quarter of another unit.
Mastering this conversion not only enhances your mathematical proficiency but also provides you with a valuable tool for solving real-world problems. Whether you are baking a cake, measuring fabric, or calculating distances, the ability to convert between improper fractions and mixed numbers will help you work more efficiently and accurately.
Now that you have a solid understanding of how to express 9/4 as a mixed number, take the next step and practice converting other improper fractions. Share your newfound knowledge with friends and family, and encourage them to explore the fascinating world of fractions. Try converting other fractions and discuss your findings in the comments below. Your active participation will not only reinforce your understanding but also help others learn and grow. What other math concepts would you like to explore?
Latest Posts
Latest Posts
-
Is Carbon Dioxide An Acid Or A Base
Nov 15, 2025
-
8 Gallons Equals How Many Cups
Nov 15, 2025
-
Do You Round Up On 5
Nov 15, 2025
-
1 Mole Of Gas At Stp
Nov 15, 2025
-
What Is A Conjecture In Math
Nov 15, 2025
Related Post
Thank you for visiting our website which covers about 9 4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.