3 Times 3 Times 3 Times 3 Times 3
sonusaeterna
Nov 16, 2025 · 8 min read
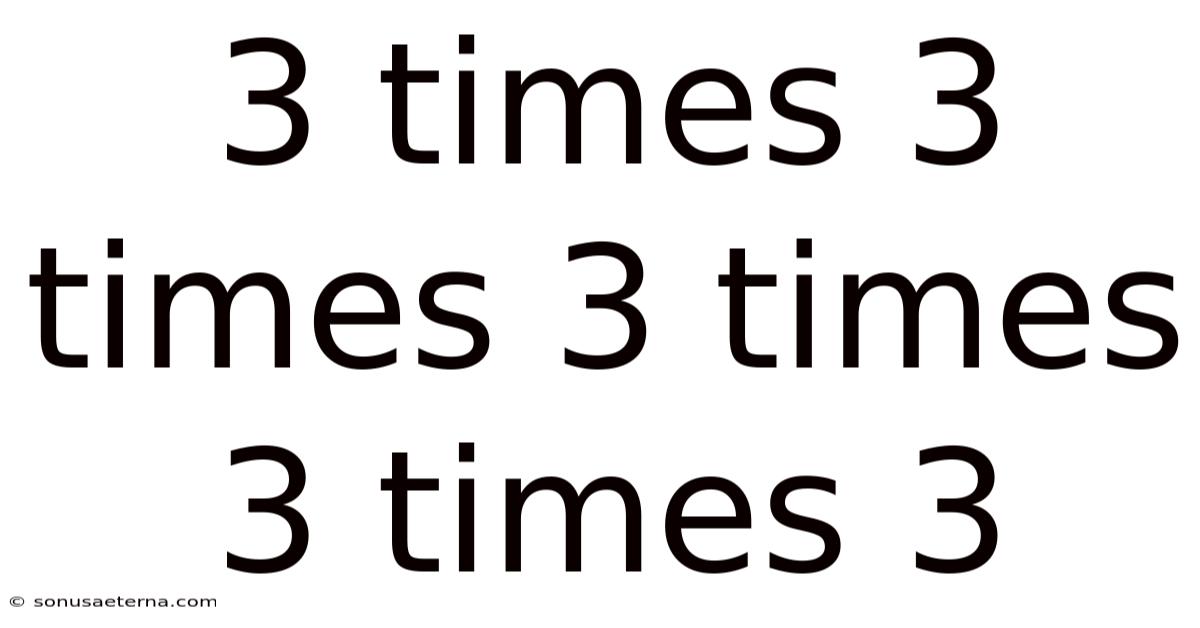
Table of Contents
Imagine you're a baker, not making cookies or cakes, but numbers. Your task is simple: take the number 3 and multiply it by itself, not just once, but five times in a row. What do you get? It seems like a trivial math question, but delving into the calculation of 3 times 3 times 3 times 3 times 3, or 3 to the power of 5, unravels fascinating insights into the world of exponents and their practical applications. This exploration will not only provide the answer but also illuminate the broader significance of exponential growth.
The concept of raising a number to a power is fundamental in mathematics and has far-reaching implications in various fields, from computer science to finance. When we talk about 3 times 3 times 3 times 3 times 3, we are essentially performing an exponentiation operation, expressed mathematically as 3^5. Understanding how to calculate this and appreciating its relevance can unlock deeper insights into how quantities scale and change in the world around us.
Main Subheading
At its core, understanding 3 times 3 times 3 times 3 times 3 involves grasping the concept of exponents. Exponents, also known as powers, are a shorthand way of expressing repeated multiplication. Rather than writing out the same number multiplied by itself multiple times, we use an exponent to indicate how many times the number is multiplied by itself. This not only saves space but also simplifies complex calculations and makes mathematical expressions more manageable.
The term 3^5 is read as "3 to the power of 5," where 3 is the base and 5 is the exponent. The base is the number being multiplied, and the exponent tells us how many times to multiply the base by itself. In this specific case, the calculation unfolds as follows: 3 * 3 * 3 * 3 * 3. This operation forms the cornerstone of many mathematical models used in science, engineering, and finance, illustrating how seemingly simple arithmetic can underpin complex analytical frameworks.
Comprehensive Overview
The operation 3 times 3 times 3 times 3 times 3 can be dissected step-by-step to fully understand the exponentiation process. First, we multiply 3 by 3, which gives us 9. Next, we multiply this result by 3 again, yielding 27. This process continues: 27 multiplied by 3 equals 81, and finally, 81 multiplied by 3 gives us the result of 243. Thus, 3^5 equals 243.
Mathematically, the exponentiation operation is written as: 3^5 = 3 * 3 * 3 * 3 * 3 = 243
The significance of this calculation goes beyond simple arithmetic. Exponential functions, like the one represented by 3^5, are crucial in describing phenomena where growth is proportional to the current size. For example, in compound interest calculations, the accumulated amount grows exponentially with each compounding period. Similarly, in biology, population growth under ideal conditions can be modeled using exponential functions.
The beauty of exponents lies in their ability to simplify complex expressions and reveal underlying patterns. Instead of laboriously multiplying a number by itself repeatedly, we can use exponential notation to express the same idea concisely. This not only makes calculations easier but also provides a more intuitive understanding of the relationships between numbers. Furthermore, understanding exponents is essential for tackling more advanced mathematical concepts such as logarithms and calculus.
The concept of exponents is not a modern invention; it has historical roots dating back to ancient civilizations. Early mathematicians recognized the need for a shorthand way to represent repeated multiplication. Over time, different notations and systems were developed, eventually leading to the modern notation we use today. The widespread adoption of exponential notation has greatly facilitated mathematical research and applications, enabling scientists and engineers to develop models and solve problems that would have been unimaginable in earlier times.
Moreover, the exponentiation operation extends beyond integer exponents. We can also have fractional or negative exponents, each with its own unique properties and applications. For example, a fractional exponent like 3^(1/2) represents the square root of 3, while a negative exponent like 3^(-1) represents the reciprocal of 3. These extensions of the exponentiation concept further enrich its versatility and applicability in various fields.
Trends and Latest Developments
In contemporary mathematics and applied sciences, the power of 3 times 3 times 3 times 3 times 3 is harnessed within more complex algorithms and computational models. Exponential calculations are critical in fields like cryptography, where the security of encryption methods often relies on the computational difficulty of reversing exponential operations. For example, the RSA encryption algorithm, widely used for secure data transmission, utilizes large prime numbers raised to various powers to ensure data security.
Another significant area is data science and machine learning. Exponential functions are used in various algorithms, such as the softmax function in neural networks, which transforms raw scores into probability distributions. Understanding how these functions behave is crucial for optimizing the performance of machine learning models. Furthermore, in financial modeling, exponential growth is a fundamental concept for projecting investment returns and assessing risk.
The ongoing trend towards big data and computational complexity has further amplified the importance of efficient exponential calculations. Modern computing systems often rely on specialized hardware and algorithms to perform these calculations quickly and accurately. For example, GPUs (Graphics Processing Units) are designed to handle parallel computations, making them well-suited for accelerating exponential operations in various applications.
Additionally, advancements in quantum computing have the potential to revolutionize the way we perform exponential calculations. Quantum computers, with their ability to exploit quantum phenomena like superposition and entanglement, could potentially solve certain exponential problems much faster than classical computers. This could have profound implications for fields like cryptography, where quantum computers could potentially break existing encryption algorithms.
From a broader perspective, the concept of exponential growth has also gained prominence in discussions about sustainability and environmental impact. The exponential growth of population, consumption, and pollution poses significant challenges to the planet's resources and ecosystems. Understanding the dynamics of exponential growth is therefore crucial for developing strategies to mitigate these challenges and promote sustainable development.
Tips and Expert Advice
To truly master the concept of 3 times 3 times 3 times 3 times 3 and its broader implications, consider these practical tips and expert advice. First, practice makes perfect. Regularly perform exponential calculations with different bases and exponents to solidify your understanding. Use online calculators or software tools to check your answers and explore the behavior of exponential functions.
Secondly, focus on understanding the underlying principles rather than just memorizing formulas. Understand why exponents work the way they do, and how they relate to other mathematical concepts. This will enable you to apply your knowledge in different contexts and solve problems more effectively. For example, understanding the laws of exponents, such as the product rule (a^m * a^n = a^(m+n)) and the power rule ((a^m)^n = a^(m*n)), can greatly simplify complex calculations.
Thirdly, explore real-world applications of exponential functions. Look for examples in finance, biology, computer science, and other fields. This will help you appreciate the relevance and importance of exponential concepts in solving real-world problems. For example, you can investigate how compound interest works, how population growth is modeled, or how encryption algorithms are designed.
Furthermore, don't be afraid to tackle more challenging problems involving exponents. Try solving equations that involve exponential terms, or explore the properties of exponential functions in calculus. This will deepen your understanding and build your problem-solving skills. For example, you can try solving equations like 2^x = 8 or exploring the derivative of the exponential function e^x.
Finally, stay curious and keep learning. Mathematics is a vast and ever-evolving field, and there's always more to discover. Read books, articles, and online resources to expand your knowledge and stay up-to-date with the latest developments. Engage with other learners and experts to share ideas and learn from their experiences. This will not only enhance your understanding of exponents but also broaden your mathematical horizons in general.
FAQ
Q: What does 3^5 mean? A: 3^5 means 3 multiplied by itself five times: 3 * 3 * 3 * 3 * 3.
Q: How do you calculate 3^5? A: Multiply 3 by itself five times: 3 * 3 = 9, then 9 * 3 = 27, then 27 * 3 = 81, and finally 81 * 3 = 243. Therefore, 3^5 = 243.
Q: Why are exponents important? A: Exponents are important because they provide a concise way to express repeated multiplication and are fundamental to many mathematical models used in science, engineering, finance, and computer science.
Q: Can exponents be fractions or negative numbers? A: Yes, exponents can be fractions or negative numbers. A fractional exponent represents a root (e.g., 3^(1/2) is the square root of 3), while a negative exponent represents a reciprocal (e.g., 3^(-1) is 1/3).
Q: Where are exponents used in real life? A: Exponents are used in various real-life applications, including compound interest calculations, population growth models, encryption algorithms, and scientific notation for expressing very large or very small numbers.
Conclusion
In summary, understanding 3 times 3 times 3 times 3 times 3, which equals 3 to the power of 5, or 243, is more than just a mathematical exercise. It represents a fundamental concept in mathematics with widespread applications across various fields. From simplifying complex calculations to modeling exponential growth in nature and finance, the power of exponents is undeniable.
By grasping the principles of exponentiation, practicing calculations, and exploring real-world applications, you can unlock deeper insights into the world around you and enhance your problem-solving skills. We encourage you to further explore the fascinating world of exponents and their applications. Take the next step in your mathematical journey and discover how exponents shape our understanding of the universe. Feel free to share your thoughts and questions in the comments below and explore related topics to deepen your knowledge.
Latest Posts
Latest Posts
-
Whats The Name Of The Yellow Teletubby
Nov 16, 2025
-
What Is A Symbol Of Bravery
Nov 16, 2025
-
What Is Robin Hoods Real Name
Nov 16, 2025
-
Compare The Earth And The Moon
Nov 16, 2025
-
Is Arabic And Aramaic The Same
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about 3 Times 3 Times 3 Times 3 Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.