1 4 Divided By 4 As A Fraction
sonusaeterna
Nov 20, 2025 · 10 min read
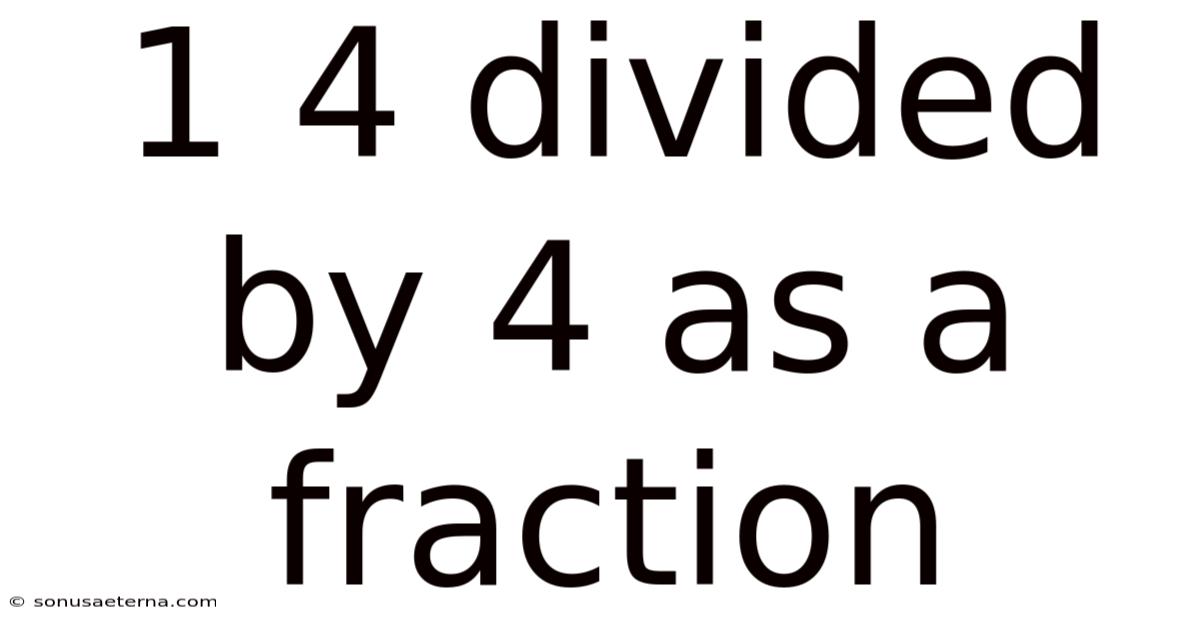
Table of Contents
Imagine you have a single delicious chocolate bar, but only a quarter of it remains. Now, you decide to share that tiny piece equally with four of your friends. How much of the entire chocolate bar does each friend get? This common scenario highlights the importance of understanding how to divide fractions, specifically when we look at 1/4 divided by 4 as a fraction.
The division of fractions might seem a little tricky at first, conjuring up images of complex equations. But, with a clear understanding of the underlying principles, it becomes surprisingly straightforward. Dividing a fraction by a whole number, such as in our example of dividing one-quarter by four, is a fundamental skill in mathematics with practical applications in everyday life, from cooking and baking to measuring and sharing. Let’s dive deep into this topic, unraveling the concepts, exploring practical applications, and answering some frequently asked questions along the way.
Understanding the Basics of Dividing Fractions
Before we tackle 1/4 divided by 4 head-on, it's crucial to grasp the fundamental concepts behind dividing fractions. Division, in its essence, is the process of splitting something into equal parts. When dealing with fractions, this means dividing a portion of a whole into smaller, equal portions. This differs slightly from dividing whole numbers, as we’re dealing with quantities that are less than one. Understanding this difference is the key to unlocking the mechanics of fraction division.
At its core, dividing fractions involves the concept of reciprocals. The reciprocal of a number is simply 1 divided by that number. For a fraction, finding the reciprocal means flipping the numerator and the denominator. For example, the reciprocal of 2/3 is 3/2. This simple flip is the magic behind dividing fractions because dividing by a fraction is the same as multiplying by its reciprocal. This principle is not just a mathematical trick; it’s a powerful tool that simplifies complex divisions into simpler multiplications.
Fractions represent parts of a whole, offering a precise way to express quantities that fall between whole numbers. They consist of two main components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. Understanding this representation is fundamental to performing operations with fractions. For example, 1/4 signifies that a whole has been divided into four equal parts, and we have one of those parts.
The concept of reciprocals is vital to understand how division of fractions works. The reciprocal of a number is simply 1 divided by that number. When we have a fraction like a/b, its reciprocal is b/a. This reciprocal becomes the key to changing a division problem into a multiplication problem, greatly simplifying calculations. For instance, if we're dividing by 1/2, we can instead multiply by 2/1, which is simply 2.
To summarize, dividing fractions relies on understanding these core principles:
- Division as splitting into equal parts: Recognize that dividing a fraction involves splitting a part of a whole into even smaller parts.
- The concept of reciprocals: Know that the reciprocal of a fraction is found by inverting the numerator and denominator.
- Dividing is multiplying by the reciprocal: Understand that dividing by a fraction is equivalent to multiplying by its reciprocal, which turns a division problem into a multiplication problem.
A Comprehensive Overview: 1/4 Divided by 4 as a Fraction
Now that we've established the foundational principles, let's focus on solving 1/4 divided by 4. The problem can be written mathematically as (1/4) ÷ 4. To solve this, we need to convert the whole number 4 into a fraction. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 4 becomes 4/1.
Now our problem is (1/4) ÷ (4/1). Here is where the reciprocal comes into play. Instead of dividing by 4/1, we multiply by its reciprocal, which is 1/4. Our equation now becomes (1/4) x (1/4).
To multiply fractions, we simply multiply the numerators together and the denominators together. So, 1 x 1 = 1, and 4 x 4 = 16. Therefore, (1/4) x (1/4) = 1/16.
This result, 1/16, represents the answer to our original problem. It means that when you divide one-quarter into four equal parts, each part is one-sixteenth of the whole. Think back to our chocolate bar example: if you divide that quarter of a chocolate bar among four friends, each friend gets one-sixteenth of the entire bar.
Let's recap the steps we took to solve this problem:
- Convert the whole number to a fraction: Express 4 as 4/1.
- Find the reciprocal: Determine the reciprocal of 4/1, which is 1/4.
- Multiply by the reciprocal: Change the division problem to a multiplication problem: (1/4) x (1/4).
- Multiply numerators and denominators: Multiply the numerators (1 x 1 = 1) and the denominators (4 x 4 = 16).
- Simplify the result: The final answer is 1/16.
Understanding these steps allows you to confidently divide fractions by whole numbers and apply this skill to various real-world scenarios.
Trends and Latest Developments in Fraction Education
Mathematics education is constantly evolving to enhance understanding and engagement. Recent trends emphasize conceptual learning and real-world applications of mathematical principles. When it comes to fractions, educators are moving away from rote memorization of rules and focusing on helping students visualize and understand what fractions represent. This shift is supported by research that shows a deeper understanding leads to better retention and application of skills.
One popular approach is the use of visual aids and manipulatives. Tools like fraction bars, pie charts, and number lines help students see fractions in a concrete way. By physically manipulating these aids, students can grasp the concept of dividing fractions more easily. For example, using a fraction bar to represent 1/4 and then dividing that bar into four equal sections allows students to visually see that each section represents 1/16 of the whole.
Another trend is the integration of technology in mathematics education. Interactive apps and online platforms offer engaging ways to practice dividing fractions. These tools often provide immediate feedback, allowing students to correct their mistakes and reinforce their understanding. Some platforms even use game-based learning to make the process more enjoyable.
In recent years, there's been increased emphasis on relating mathematical concepts to real-life scenarios. This helps students understand the relevance of what they're learning and makes it more meaningful. For instance, teachers might use cooking recipes to illustrate the division of fractions. If a recipe calls for 1/2 cup of flour and you want to make half the recipe, you need to divide 1/2 by 2, which results in 1/4 cup of flour.
Educators are also focusing on addressing common misconceptions about fractions. One common misconception is that dividing always results in a smaller number. When dividing a fraction by a whole number, the result is indeed smaller, but understanding why this happens is crucial. By explicitly addressing these misconceptions and providing clear explanations, educators can help students build a stronger foundation in fractions.
Tips and Expert Advice for Mastering Fraction Division
Mastering fraction division requires more than just memorizing rules; it involves developing a deep understanding of the underlying concepts. Here are some practical tips and expert advice to help you confidently tackle fraction division problems:
- Visualize the Problem: One of the most effective ways to understand fraction division is to visualize what's happening. Use diagrams, drawings, or physical objects to represent the fractions involved. For example, if you're dividing 1/2 by 3, draw a rectangle, divide it in half, and then divide that half into three equal parts. You'll see that each part represents 1/6 of the whole.
- Practice Regularly: Like any mathematical skill, practice is key to mastering fraction division. Work through a variety of problems, starting with simple examples and gradually progressing to more complex ones. Use online resources, textbooks, or worksheets to find practice problems. The more you practice, the more comfortable you'll become with the process.
- Understand the "Why," Not Just the "How": Don't just memorize the rule of "invert and multiply." Take the time to understand why dividing by a fraction is the same as multiplying by its reciprocal. This understanding will help you remember the rule and apply it correctly in different situations. This can be achieved by going back to the core principles and visual models discussed previously.
- Use Real-World Examples: Connect fraction division to real-world scenarios to make it more meaningful. Think about situations where you might need to divide a fraction, such as sharing food, measuring ingredients, or splitting costs. By seeing how fractions are used in everyday life, you'll better understand their relevance and importance.
- Check Your Work: After solving a fraction division problem, always check your work to make sure your answer is reasonable. Use estimation to get a rough idea of what the answer should be, and then compare your calculated answer to your estimate. If your answer seems way off, go back and review your steps to find any errors. For instance, consider whether the answer should be smaller or larger than the original fraction, and use this logic to evaluate the result.
FAQ: Dividing 1/4 by 4
Q: Why do we use the reciprocal when dividing fractions?
A: Dividing by a number is the same as multiplying by its inverse. The reciprocal of a fraction is its inverse. Using the reciprocal allows us to convert a division problem into a multiplication problem, which is often easier to solve.
Q: Can I use a calculator to divide fractions?
A: Yes, calculators can be helpful for dividing fractions, especially for complex problems. However, it's important to understand the underlying concepts so you can interpret the results correctly.
Q: What if I'm dividing a fraction by a mixed number?
A: First, convert the mixed number to an improper fraction. Then, proceed with the division as usual by multiplying by the reciprocal of the improper fraction.
Q: Is there a visual way to understand 1/4 divided by 4?
A: Yes! Imagine a pie cut into four equal slices (each representing 1/4). Now, imagine dividing one of those slices into four smaller, equal pieces. Each of those smaller pieces represents 1/16 of the whole pie.
Q: How does this concept apply to real life?
A: Imagine you have a quarter of an hour (15 minutes) to complete four tasks. Dividing 1/4 of an hour by 4 tells you how much time you can spend on each task – in this case, 1/16 of an hour, or about 3.75 minutes.
Conclusion
Understanding how to divide fractions, particularly 1/4 divided by 4 as a fraction, is a fundamental skill with practical applications in various aspects of life. By grasping the concepts of reciprocals, visualizing the problem, and practicing regularly, you can confidently tackle fraction division problems. Remember, the key is to understand the "why" behind the rules, not just the "how."
Now that you have a solid understanding of dividing fractions, put your knowledge to the test. Practice with different fractions and real-world scenarios. Share your newfound skills with friends and family. And, most importantly, continue to explore the fascinating world of mathematics!
Latest Posts
Latest Posts
-
How Wide Is The Great Pyramid Of Giza
Nov 20, 2025
-
What Is A Constituent In Linguistics
Nov 20, 2025
-
Do The Easter Island Heads Have Bodies
Nov 20, 2025
-
What Is An Act Of Supremacy
Nov 20, 2025
-
What Is The Color Of A Whale Shark
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about 1 4 Divided By 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.