1/3 Cup + 1/3 Cup Equals How Many Cups
sonusaeterna
Nov 16, 2025 · 9 min read
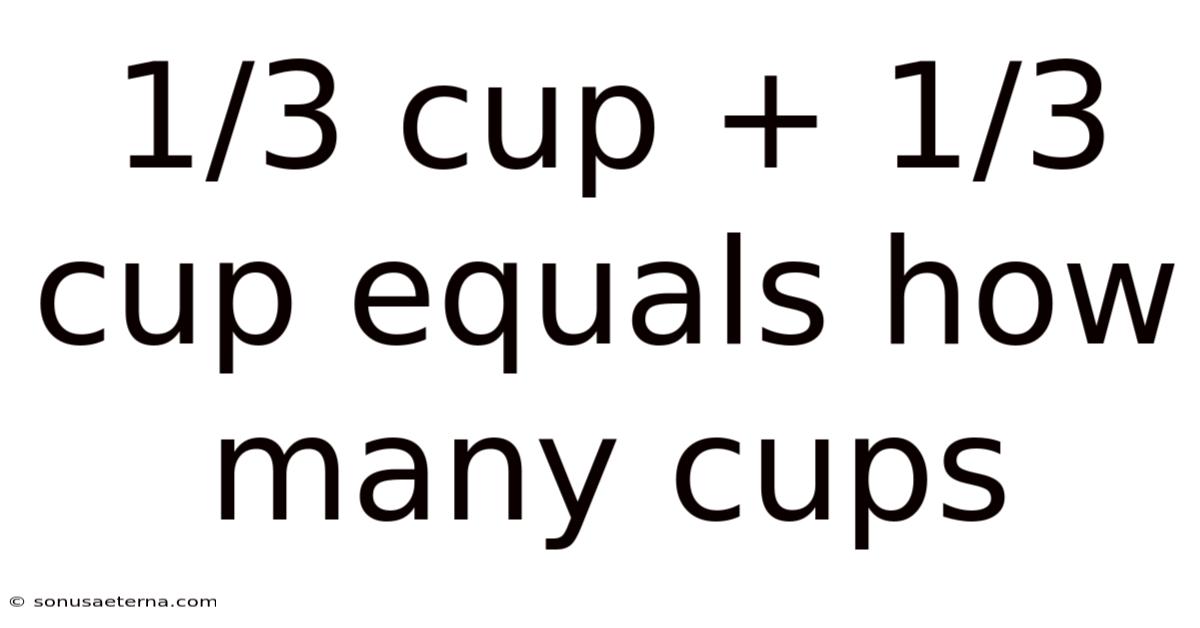
Table of Contents
Imagine you're baking your favorite chocolate chip cookies. The recipe calls for a precise amount of flour, sugar, and of course, chocolate chips. You carefully measure out 1/3 cup of flour and then another 1/3 cup. The question pops into your head: how much flour have I added in total? This seemingly simple query leads us to the heart of fractions and how they work in our everyday lives.
Understanding how to combine fractions like 1/3 cup + 1/3 cup isn't just about baking; it's a fundamental skill that applies to various situations. Whether you're dividing a pizza, sharing snacks with friends, or even calculating proportions in a more complex scenario, knowing how to add fractions is essential. Let’s dive into a comprehensive exploration of this topic, making sure you're confident and clear about the answer and the underlying principles.
Main Subheading
Adding fractions, especially those with common denominators, is a straightforward process once you grasp the core concept. In the case of 1/3 cup + 1/3 cup, we’re dealing with fractions that already share the same denominator, which simplifies the calculation. However, understanding why we can simply add the numerators together is crucial.
Before diving into the specifics, it’s helpful to visualize what a fraction represents. The denominator (the bottom number) tells us how many equal parts the whole is divided into, while the numerator (the top number) tells us how many of those parts we have. In our scenario, the denominator is 3, meaning the whole cup is divided into three equal parts.
Comprehensive Overview
Definitions and Basics
At its core, a fraction represents a part of a whole. It consists of two primary components:
- Numerator: This is the number above the fraction bar, indicating how many parts of the whole are being considered.
- Denominator: This is the number below the fraction bar, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator is 1, and the denominator is 3. This means we have one part out of a total of three equal parts.
Scientific Foundations
The concept of fractions dates back to ancient civilizations. Egyptians used fractions extensively in their measurements and calculations, primarily using unit fractions (fractions with a numerator of 1). The Babylonians used a base-60 system, which also involved fractions. The formalization of fraction arithmetic, as we know it today, evolved over centuries, with significant contributions from Greek and Indian mathematicians.
The mathematical principle behind adding fractions relies on the idea that we can only directly add quantities that are expressed in the same units. When fractions have the same denominator, they are already expressed in the same "units" (in this case, thirds), making addition straightforward.
Adding Fractions with Common Denominators
When adding fractions with common denominators, the process is simple:
- Keep the denominator: Since the denominators are the same, the resulting fraction will also have the same denominator.
- Add the numerators: Add the numerators together to find the new numerator of the resulting fraction.
In our case, 1/3 + 1/3 follows this rule directly. We keep the denominator (3) and add the numerators (1 + 1), giving us 2/3. Thus, 1/3 cup + 1/3 cup = 2/3 cup.
Visual Representation
Visualizing fractions can make the concept even clearer. Imagine a pie cut into three equal slices. Each slice represents 1/3 of the pie. If you have one slice (1/3) and you add another slice (1/3), you now have two slices out of the three, which is 2/3 of the pie.
Real-World Examples
Fractions are everywhere in our daily lives. Here are a few examples:
- Cooking: Recipes often call for fractional amounts of ingredients, such as 1/2 teaspoon of salt or 3/4 cup of sugar.
- Time: An hour is often divided into fractions, such as 1/4 hour (15 minutes) or 1/2 hour (30 minutes).
- Measurements: Measuring lengths, weights, or volumes often involves fractions, such as 1/8 inch or 2/3 pound.
- Sharing: When sharing a pizza or a cake, you often divide it into fractions to distribute it among people.
Why Common Denominators Matter
The reason we need common denominators when adding fractions is that we are essentially adding different "units" if the denominators are different. For example, it wouldn't make sense to directly add 1/2 and 1/4 without first converting them to a common denominator. We need to express both fractions in terms of the same-sized parts to accurately add them together. The common denominator for 1/2 and 1/4 is 4. We convert 1/2 to 2/4, and then we can add 2/4 + 1/4 to get 3/4. This principle is fundamental to all fraction arithmetic.
Trends and Latest Developments
While the basic principles of fractions remain constant, their application evolves with technological and educational advancements.
Educational Approaches
Modern educational approaches emphasize visual and hands-on learning to help students grasp fractions more intuitively. Tools like fraction bars, pie charts, and interactive software are used to illustrate fractional concepts. These methods aim to make learning about fractions more engaging and less abstract.
Digital Tools
Numerous apps and websites offer interactive lessons and practice exercises for mastering fractions. These digital tools often include gamified elements to make learning fun and provide immediate feedback to learners. They cater to various learning styles and can be particularly helpful for students who struggle with traditional methods.
Data Analysis and Fractions
In data analysis, fractions play a crucial role in calculating proportions, percentages, and ratios. Understanding fractions is essential for interpreting statistical data and making informed decisions. For example, market share data often involves fractional representations of total sales.
Popular Opinions and Misconceptions
Despite the importance of fractions, many people still struggle with them. Common misconceptions include:
- Adding both numerators and denominators: Some people mistakenly add both the numerators and denominators when adding fractions (e.g., thinking 1/2 + 1/2 = 2/4).
- Difficulty visualizing fractions: Abstract understanding without visual aids can lead to confusion.
- Equating fractions to whole numbers: Not recognizing that fractions represent parts of a whole can hinder comprehension.
Addressing these misconceptions through clear explanations and visual aids is crucial for building a strong foundation in fraction arithmetic.
Tips and Expert Advice
Simplify Fractions
Always simplify fractions to their lowest terms. For example, if you end up with 2/4, simplify it to 1/2. This makes the fraction easier to understand and work with in further calculations. Simplifying fractions involves dividing both the numerator and the denominator by their greatest common factor (GCF). In the case of 2/4, the GCF is 2, so dividing both by 2 gives us 1/2.
Use Visual Aids
Visual aids can be incredibly helpful, especially when learning or teaching fractions. Draw diagrams, use fraction bars, or even cut up a pie to physically represent the fractions. Seeing the fractions in a tangible way can make the concepts much clearer. This is particularly effective for students who are visual learners.
Practice Regularly
Like any mathematical skill, mastering fractions requires regular practice. Work through various problems, starting with simple ones and gradually moving to more complex ones. Use online resources, textbooks, or create your own practice problems. Consistent practice builds confidence and reinforces understanding.
Relate to Real-World Scenarios
Connect fractions to real-world situations to make them more relevant and understandable. Use examples from cooking, time management, or sharing to illustrate how fractions are used in everyday life. This helps to contextualize the mathematical concepts and makes them more meaningful.
Break Down Complex Problems
If you encounter a complex problem involving fractions, break it down into smaller, more manageable steps. Identify the individual fractions and operations involved, and tackle them one at a time. This approach can make the problem less daunting and easier to solve.
Understand Equivalent Fractions
Make sure you understand the concept of equivalent fractions. Equivalent fractions are fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 = 2/4 = 3/6). Being able to convert between equivalent fractions is essential for adding fractions with different denominators.
Don't Be Afraid to Ask for Help
If you're struggling with fractions, don't hesitate to ask for help. Seek out a teacher, tutor, or knowledgeable friend who can provide guidance and support. Sometimes, a different explanation or perspective can make all the difference.
FAQ
Q: What does 1/3 mean?
A: 1/3 means one part out of three equal parts that make up a whole.
Q: Can you add fractions with different denominators?
A: Yes, but you need to find a common denominator first. Convert each fraction to an equivalent fraction with the common denominator, and then add the numerators.
Q: What is a common denominator?
A: A common denominator is a number that is a multiple of the denominators of two or more fractions. It allows you to add or subtract the fractions.
Q: How do you simplify a fraction?
A: To simplify a fraction, divide both the numerator and the denominator by their greatest common factor (GCF).
Q: What is an improper fraction?
A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/3).
Q: How do you convert an improper fraction to a mixed number?
A: Divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the new numerator, and the denominator stays the same (e.g., 5/3 = 1 2/3).
Q: Why are fractions important?
A: Fractions are essential for representing parts of a whole and are used in various real-world applications, including cooking, measurements, and data analysis.
Conclusion
So, to answer the initial question definitively: 1/3 cup + 1/3 cup equals 2/3 cup. This simple calculation is a gateway to understanding the broader world of fractions and their significance in everyday life. By grasping the basic principles of fractions, using visual aids, practicing regularly, and connecting them to real-world scenarios, anyone can master these fundamental mathematical concepts.
Ready to put your newfound knowledge to the test? Try baking a recipe that requires fractional measurements or share a pizza with friends, ensuring everyone gets their fair share. Engage with online resources and practice problems to solidify your understanding. Share this article with friends or family who might also benefit from a clearer understanding of fractions. Let's spread the knowledge and make math a little less daunting for everyone!
Latest Posts
Latest Posts
-
How To Say Hard In Spanish
Nov 16, 2025
-
What Is A Special Ed Class
Nov 16, 2025
-
Windows Batch File If Then Else
Nov 16, 2025
-
Who Are The Careers In The Hunger Games
Nov 16, 2025
-
What Is A Bunch Of Penguins Called
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Cup + 1/3 Cup Equals How Many Cups . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.